Definizioni
Prova è l'esecuzione di un esperimento.
U, insieme universo delle probabilità, associato ad un dato esperimento, è l'insieme dei risultati possibili.
Evento è un insieme di risultati possibili, ovvero un sottoinsieme di U.
Evento elementare è sottoinsieme di U con un solo elemento.
Evento certo, è quello che si realizza sempre.
Evento impossibile, è quello che non si realizza mai.
EsempioProva: lancio di 8 monete
U insieme universo:(9 risultati possibili): 8 teste; 7 teste 1 croce; 6 teste 2 croci; 5 teste 3 croci; 4 teste 4 croci; 3 teste 5 croci; 2 teste 6 croci; 1 testa 7 croci; 8 croci.
Evento: escono almeno 2 teste.
Evento elementare: escono 2 teste e 6 croci.
Evento certo: escono al massimo 8 teste.
Evento impossibile: escono almeno 9 teste.
Concezione frequentistica
Si esegue un grande numero di prove. Per esempio si fanno 10000 lanci con 8 monete e si conta la frequenza assoluta, ovvero gli "n" casi in cui sono uscite 2 teste e 6 croci, quindi si calcola la probabilità attraverso il rapporto n/10000. In questo modo la probabilità assume l'aspetto di frequenza relativa.
Concezione classica
La probabilità è uguale al rapporto tra i casi favorevoli ad un certo evento E ed i casi possibili pensati come egualmente probabili. Per esempio se l'esperimento è il lancio di 8 monete, il numero dei casi possibili è 28=256. Se l'evento è: uscita di 2 teste e 6 croci, il numero dei casi favorevoli è 28, ossia il numero che si trova nel ottava riga, seconda diagonale del triangolo di Tartaglia Pascal. La probabilità quindi che lanciando 8 monete, escano 2 teste e 6 croci è: P(E)=28/256. Si tenga presente che la probabilità è un numero razionale compreso tra 0 e 1 ovvero 0≤P(E)≤1.
Nella tabella sono riportati i grafici della frequenza relativa e della probabilità dell'esperimento: lancio di otto monete. Tramite il foglio elettronico (con la variabile "casuale") si sono simulati 500 lanci di otto monete e si è conteggiato (con la funzione "conta.se") il numero di volte che si è verificato l'evento: 0 teste 8 croci, 1 testa 7 croci, 2 teste 6 croci, 3 teste 5 croci, 4 teste 4 croci, 5 teste 3 croci, 6 teste 2 croci, 7 teste 1 croce, 8 teste 0 croci. La frequenza relativa si è calcolata dividendo la frequenza assoluta per 500. Per il calcolo della probabilità invece i casi possibili sono i numeri della ottava riga del triangolo: 1, 8, 28, 56, 70, 56, 28, 8, 1, i casi possibili sono 28=256.
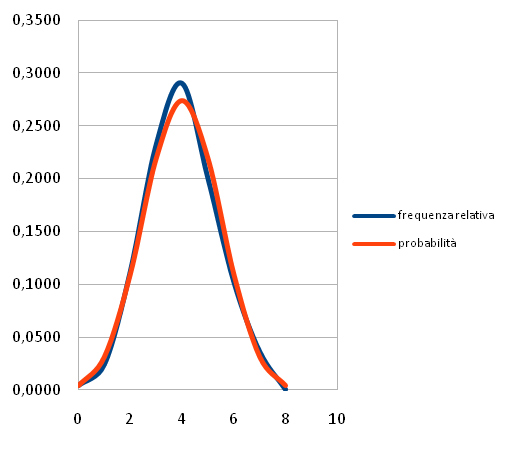
La probabilità è stata calcolata quindi: P(E)=casi possibili/casi favorevoli. Se avessimo fatto la simulazione di 10000 lanci i due grafici sarebbero risultati praticamente sovrapposti. Si noti ancora che si tratta di grafici a "campana" con picco sull'evento 4 teste e 4 croci che ovviamente è il più probabile. Però c'è da sottolineare che non tutti gli eventi sono ripetibili; ad esempio, una partita di pallacanestro di cui vogliamo calcolare la probabilità della vittoria della squadra X contro la squadra Y.
La definizione di probabilità applicabile ad esperimenti casuali i
cui eventi elementari non siano ritenuti ugualmente possibili e che non siano necessariamente ripetibili più
volte sotto le stesse condizioni è dovuta ad Bruno de Finetti.
Bruno De Finetti, che ha insegnato
matematica anche all'università degli studi di Trieste,
dove c'è un'aula a lui dedicata, ha proposto la concezione soggettiva della probabilità.
Concezione soggettiva
La definizione di probabilità applicabile ad esperimenti casuali i cui eventi elementari non siano ritenuti ugualmente possibili e che non siano necessariamente ripetibili più volte sotto le stesse condizioni è dovuta ad Bruno de Finetti. Bruno De Finetti, che ha insegnato matematica anche all'università degli studi di Trieste, dove c'è un'aula a lui dedicata, ha proposto la concezione soggettiva della probabilità.
Definizione di probabilità in senso soggettivo: la probabilità di un evento è il prezzo che un individuo ritiene equo pagare per ricevere 1 se l'evento si verifica, 0 se l'evento non si verifica.
Esempio: se penso che le probabilita' di vincita in una partita di pallacanestro della squadra X contro la squadra Y siano del 60%, devo essere disposto a puntare 60 euro, sulla sua vincita, per riceverne 100 in caso di vittoria e perdendo tutto in caso di sconfitta. E' fondamentale, che devo avere il maggior numero di informazioni possibili e, tramite esse, devo attribuire determinate probabilita' a determinati eventi. Nel caso specifico devo sapere come sono in classifica, chi gioca in casa, se ci sono giocatori assenti per infortunio, qual'è lo stato di forma delle due squadre ecc.. ecc..