Triangolo di Tartaglia
In opere cinesi del 1100 a.c. circa si fa riferimento a sistemi di tabulazione per coefficienti dello sviluppo della potenza di un binomio: è verosimile che quella tabella di numeri, nota in occidente con il nome di "triangolo di Pascal" o "triangolo di Tartaglia" abbia avuto origini in Cina intorno a tale data.
| 1 | ||||||||||||||||||
| 1 | 1 | |||||||||||||||||
| 1 | 2 | 1 | ||||||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
Proprietà del triangolo
Sono due le proprietà che presenta questo famoso triangolo.
La prima è data dalla simmetria del triangolo che può essere riassunta dalla seguente formula:
C(n,k)=C(n,n-k)
La seconda proprietà è che, ogni numero di una certa riga è dato dalla somma dei due numeri che si trovano nella precedente riga, il primo nella stessa diagonale, il secondo nella diagonale sucessiva. Questa caratteristica si riassume nella seguente formula:
C(n,k)=C(n-1,k)+C(n-1,k-1)
I numeri del triangolo rappresentano le "combinazioni" ovvero il numero di sottoinsiemi di k elementi in un insieme di n elementi.
Sviluppo del binomio
Il triangolo di Tartaglia consente di individuare i coefficienti dello sviluppo di un binomio (a+b) elevato alla n-esima potenza. I coefficienti dei singoli termini sono dati dai numeri della (n+1)-esima riga del triangolo. Proponiamoci di sviluppare l'espressione (x+y)2, dove n è un intero positivo (potenza n-sima del binomio). Sappiamo che si ha (x+y)2 =x2 + 2xy + y2 e con un semplice calcolo si trova: (x+y)3 =x3+3x2y+3xy2+ y3
I monomi che si ottengono dallo sviluppo di (x+y)2 e di (x+y)3 li possiamo rappresentare mediante un grafo simile a quello della figura
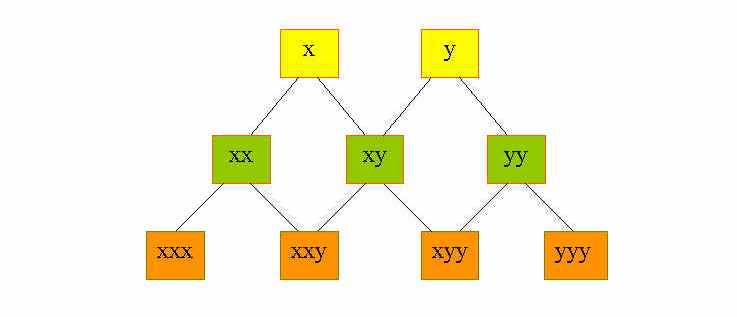
ad ogni cammino sul grafo corrisponde un monomio, per esempio il percorso sinistra sinistra destra partendo da sopra corrisponde al monomio xxy. Il grafo sembra analogo a quello che rappresenta il lancio della moneta. Per la proprietà commutativa della moltiplicazione, due monomi contenenti lo stesso numero di volte le x, e le y, diventano simili. Ad esempio, i due monomi xyx e xxy sono simili. Il problema è allora quello di contare i monomi che diventano simili traloro. Conviene quindi modificare il grafo facendo confluire in uno stesso vertice i cammini che corrispondono a monomi simili. Il nostro problema si riduce a quello di contare il numero dei cammini che arrivano ad un dato vertice in un grafo come quello della figura. Teniamo presente che, quando conteggiamo dei percorsi, intendiamo sempre che si parte da sopra e si percorre la via più breve per arrivare ad un certo incrocio.
Possiamo concludere così: lo sviluppo di (x+y)n è costituito dalla somma di tutti i monomi del tipo xn-k yk moltiplicati per i coefficienti (n,k) che sono i numeri del triangolo di Tartaglia-Pascal.
Ricordiamo che è: (n,n) = (n,0) = 1 (n,1) = (n,n-1) = n
Indichiamo con n il numero delle righe,
tenendo presente che la prima riga, quella con il solo numero 1 è la riga zero. Indichiamo con k il numero delle diagonali,
tenendo presente che la prima diagonale, quella formata da tutti numeri 1, è la diagonale zero.
Sviluppando (x+y)5 otteniamo x5+5x4y+10x3y2+10x2y3+5xy4+y5.