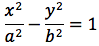Le coniche
Le coniche da un punto di vista geometrico
Supponiamo di avere una retta a, ed una retta g incidente ad a . Supponiamo che l'angolo formato dalle due rette non sia retto. Il "cono circolare retto a due falde" è definito come la superficie generata dalla rotazione della retta g, che è chiamata generatrice, intorno alla retta a che costituisce quindi l'asse di rotazione.
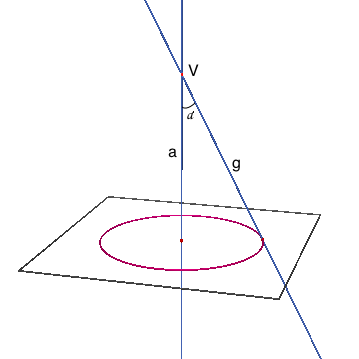
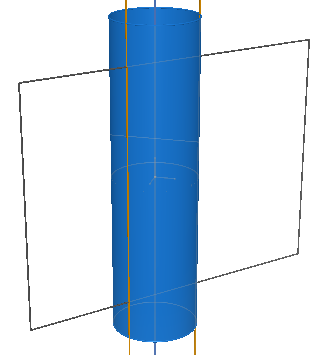
Il punto V di intersezione tra a e g è detto "vertice" del cono. L'angolo α formato da g con a è detto "semiapertura" del cono. Il cono è, per come è stato definito, un cono infinito, a due falde, unite per il vertice. La parte di cono compresa tra il vertice e una sezione si chiama cono finito. Se la sezione è normale, si definisce cono finito retto. Se la retta generatrice è parallela all'asse, la superficie ottenuta si chiama "cilindro circolare retto" Il cilindro può essere considerato come un particolare cono, in tal caso il vertice stà all'infinito. Si chiamano coniche non degeneri le curve che si ottengono intersecando una superficie conica con un piano non passante per il vertice del cono. Si chiamano coniche degeneri le curve che si ottengono intersecando una superficie conica con un piano passante per il vertice del cono.
Una conica è la curva ottenuta intersecando un cono circolare retto con un piano. Chiamiamo x l'angolo formato dal piano secante con la retta generatrice e con α la semiapertura del cono, distinguiamo i seguenti tipi di coniche: circonferenze, ellissi, parabole ed iperboli si distinguono a seconda di come è disposto il piano che seziona il cono. Se prendiamo un piano passante per il vertice otteniamo una cosiddetta conica degenere. Vediamo ora i vari casi possibili di sezioni coniche degeneri. Pensiamo innanzitutto di sezionare un cilindro, che come si è visto, può essere pensato come un particolare cono. Il piano non taglia il cilindro: non si ottiene nessuna conica reale. Il piano taglia il cilindro ed è parallelo all'asse di rotazione: conica degenere in due rette distinte parallele.
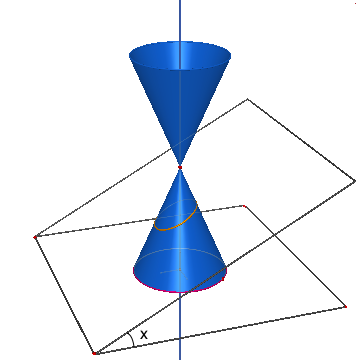
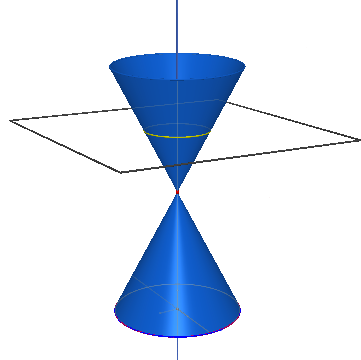
E' ottenuta dall'intersezione del cono con un piano che ha l'angolo x=0, perpendicolare quindi al suo asse. La circonferenza è una curva chiusa ed è una contenuta in una sola delle due falde del cono. La circonferenza degenere si riduce ad un solo punto, il vertice.
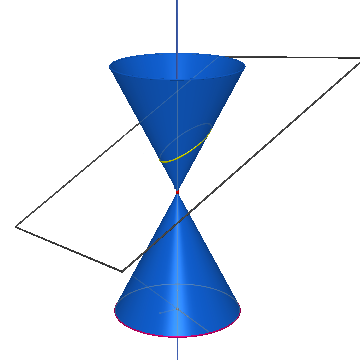
E' ottenuta intersecando il cono con un piano, che con il suo asse formi un angolo compreso tra: α⟨x⟨π/2. L'ellisse è una curva contenuta in una sola delle due falde del cono ed è una curva chiusa. L'ellisse degenere si riduce ad un solo punto, il vertice.
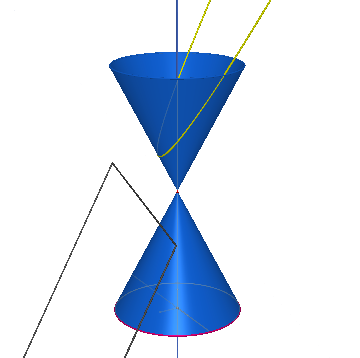
E' ottenuta per intersezione del cono con un piano che ha l'angolo x=α, parallelo quindi alla retta generatrice. La parabola appartiene a una sola delle falde del cono e non è una curva chiusa. La parabola degenere si riduce a due rette coincidenti in quanto il piano che seziona il cono, passando per il vertice ed essendo parallelo alla generatrice, risulta tangente al cono.
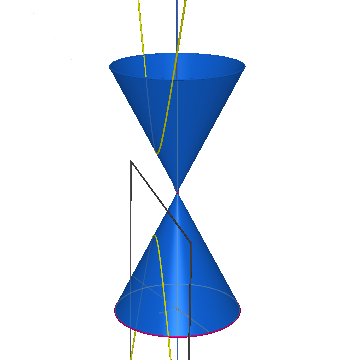
E' ottenuta per intersezione del cono con un piano che formi con il suo asse un angolo compreso tra: α⟨x≤π/2. L'iperbole è una curva aperta ed appartiene ad entrambe le falde del cono, in quanto il piano le interseca. L'iperbole degenere si riduce ad una coppia distinta di rette incidenti nel vertice che risultano essere due generatrici del cono.




Le coniche da un punto di vista algebrico
Le equazioni di secondo grado in due incognite sono costituite da una somma di sei termini:
ax2+bxy+cy2+dx+ey+f=0Queste equazioni sono di diversi tipi, alcune non ammettono soluzioni reali, altre ammettono solo una soluzione, altre ancora sono indeterminate e ammettono infinite soluzioni. Tenendo presente che una soluzione è una coppia ordinata di valori, riportando nel piano cartesiano queste coppie ordinate, otteniamo dei punti che costituiscono una conica. Le coniche degeneri come quelle non degeneri, riferite ad un sistema di assi cartesiani ortogonali, si esprimono dunque, mediante funzioni algebriche di secondo grado. L'aspetto algebrico delle coniche degeneri, iperboli e parabole, risulta il prodotto di due equazioni di primo grado. L'equazione di un'iperbole degenere si avrà moltiplicando membro a membro le equazioni sotto forma implicita delle due rette incidenti nel vertice; Es. Le due rette di equazione x=0, y=0, costituiscono l'iperbole degenere di equazione xy=0 l'equazione di una parabola degenere si ottiene innalzando al quadrato i due membri dell'equazione, in forma implicita, della retta. La retta di equazione 2x+4y-1=0 presa due volte dà luogo alla parabola degenere (2x+4y-1)²=0 L'equazione di un'ellisse degenere è data da quella di un'ellisse che si riduce ad un solo punto. L'ellisse di equazione x2+2y2=0 corrisponde all'origine Segnaliamo ora alcuni esempi di coniche degeneri, dopo aver ricordato che dal punto di vista analitico una conica è degenere se l'equazione che la rappresenta è soddisfatta da un unico punto reale (esempio 3x2 + 5y2 = 0) oppure se il polinomio che la individua è scomponibile.
1) Conica degenere in due rette reali distinte x (x+y) = 0 (tipo iperbolico) (x - 1 ) ( x + 1) = 0 (tipo parabolico) 2) conica degenere in due rette reali coincidenti (x + y +1)(x + y + 1) = 0 Segnaliamo ora un esempio di conica completamente immaginaria: 3x2 + 4y2 = -1 Ovviamente non esiste alcuna coppia di numeri reali (x;y) che soddisfa l'equazione. Ripetiamo che tale conica è detta ellisse immaginaria perchè, come vedremo, rientra nel tipo ellittico.Le equazioni di secondo grado in due incognite hanno diverse sfacettature, alcune non ammettono soluzioni reali come x2+xy+y2+4=0, altre ammettono solo una soluzione x2+y2=0, altre, come per esempio come x2+4xy+4y2-9=0 sono date dal prodotto tra due rette (x+2y+3)(x+2y-3)=0. Altre equazioni sono indeterminate ovvero ammettono infinite soluzioni, tenendo sempre presente che una soluzione è una coppia ordinata di valori, riportando nel piano cartesiano queste coppie ordinate, otteniamo dei punti che costituiscono una conica.
Tutto ciò è in accordo con il fatto che se intersechiamo un cono a due falde con un piano passante per l'asse di simmetria, si determinano due rette, se il piano passa per il vertice del cono si determina un solo punto, se il piano contiene la generatrice del cono si determina una retta corrispondente proprio alla generatrice e queste sono dette coniche degeneri.Come riconoscere una conica dalla relativa equazione
La conica di equazione ax2+bxy+cy2+dx+ey+f=0
é una parabola, eventualmente degenere in due rette parallele se: b2-4ac=0 é un'ellisse (eventualmente immaginaria oppure degenere in un punto) se: b2-4ac<0 é una'iperbole, eventualmente degenere in due rette incidenti se: b2-4ac > 0.OSSERVAZIONE Una conica é quindi una parabola (eventualmente degenere in due rette parallele) se e solo se il complesso dei termini di secondo grado é un quadrato perfetto; una parabola ha quindi equazione del tipo
(ax+by)2+cx+dy+e=0
Si dimostra che la retta di equazione ax+by = 0 é parallela all'asse della parabola. Essendo l'equazione di una conica individuata da 5 parametri una conica generica sara' individuata da 5 punti il ciò equivale a dire che per 5 punti passa una ed una sola conica Essendo l'equazione di una conica non tanto semplici da trattare, alcune coniche si studiano in posizioni particolari: come ad esempio le ellissi con asse orizzontale o le parabole con asse verticaleLe coniche da un punto di vista fisico
Dal punto di vista fisico, l'orbita descritta da una particella carica che entra in un campo magnetico uniforme è una circonferenza.
Dal punto di vista fisico l'orbita descritta da un pianeta è un'ellisse, per esempio la terra, ruotando attorno al sole descrive un'ellisse in cui, il sole stesso, corrisponde ad uno dei due fuochi. I moti dei pianeti avvengono quindi su un piano, detto piano orbitale.
Dal punto di vista fisico la parabola è la traiettoria a cui è costretto un proiettile, soggetto alla forza gravitazionale.
Dal punto di vista fisico se un corpo arriva nella sfera gravitazionale di un pianeta con una velocità sufficientemente elevata, si allontana seguendo una traiettoria iperbolica di cui il pianeta stesso rappresenta il fuoco.
Le coniche come luoghi geometrici
L'equivalenza fra la definizione delle coniche come intersezioni nello spazio di un cono circolare retto a due falde con un piano e la loro definizione come luoghi geometrici nel piano è stato chiarito dal matematico parigino Germinal Pierre Dandelin, attraverso un teorema che porta il suo nome. Dandelin nacque in pieno periodo rivoluzionarionato (1794-1847) e combattè per Napoleone, durante i cento giorni lavorò per il Ministero degli Interni agli ordini di Lazare Carnot. Dopo la sconfitta di Napoleone a Waterloo nel 1815 si rifugiò nel Belgio e nel 1817 diventò cittadino olandese.
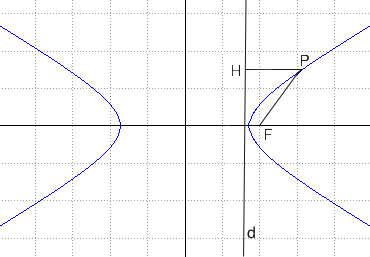
C'è una definizione che accomuna tutte le coniche (non degeneri). Dato un punto F, fuoco ed una retta d, direttrice, non contenente F, chiamata d(F;P) la distanza di un punto P della conica dal fuoco e chiamata d(H;P) la distanza del punto P della direttrice
Definizione: Conica è il luogo geometrico del piano costituita dai punti P tali che il rapporto d(F;P)/d(P;H) è costante
tale costante "e" si chiama eccentricità della conica.
Per e = 0 si ottiene una circonferenza
Per 0 < e < 1 si ottiene un'ellisse
Per e = 1 una parabola
per e > 1 una iperbole.
Da questa definizione generale di conica basata sull'eccentricità si può dimostrare che ne conseguono le definizioni specifiche di conica che vedremo in seguito.
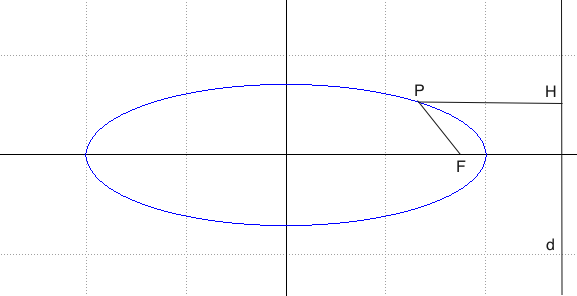
Per una ellisse e una iperbole si possono assumere due coppie fuoco, direttrice, da cui deriva la stessa curva.
Nel caso della circonferenza e = 0 e si deve immaginare che la retta direttrice sia a distanza infinita dal fuoco. Il caso della circonferenza va trattato come caso limite di ellisse in quanto se l'eccentricità è zero la direttrice deve allontanarsi all'infinito. Si può dunque affermare che l'eccentricità di una sezione conica dia una misura di quanto essa si allontani dall'essere circolare. Per una data lunghezza del semiasse maggiore, quanto più si avvicina a 1, tanto più piccolo è il semiasse minore consistente in tutti i punti la cui distanza da F è uguale al prodotto di e per la rispettiva distanza dalla direttrice d.
Circonferenza
Definizione: la circonferenza è il luogo geometrico dei punti equidistanti dal centro.
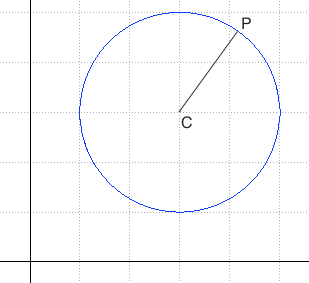
Per determinare l'equazione della circonferenza imponiamo quindi che la distanza del punto generico P(x,y) dal centro C(x0,y0) sia uguale al raggio r.
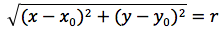
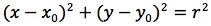
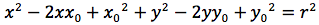
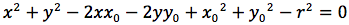
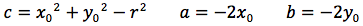
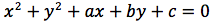
Affinché un'equazione di secondo grado a due incognite, rappresenti una circonferenza, è necessario e sufficiente quindi, che non ci sia il termine in xy, che i coefficienti di x2 e y2 siano uguali ed infine che x02+y02-c sia un valore positivo.
Ellisse
Definizione: l'ellisse e' il luogo geometrico dei punti del piano per cui e' costante la somma delle distanze da due punti fissi detti fuochi
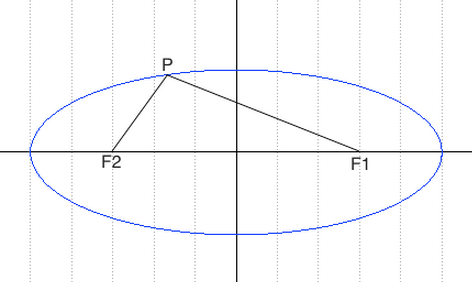
Per tutti i punti P della figura avremo che d(P;F1)+d(P;F2)=costante.
Per sapere quanto vale la costante spostiamo il punto P fino a portarlo sull'asse orizzontale, allora si vede che la somma d(P;F1)+d(P;F2) e' uguale alla distanza fra i due punti dell'ellisse che tagliano l'asse delle x (asse orizzontale). Chiamiamo questa distanza 2a (a per indicare che e' una costante e 2 perche', essendo l'ellisse simmetrica spesso ci servira' la meta' della distanza, cioe' il semiasse orizzontale); quindi avremo per tutte le ellissi d(P;F1) + d(P;F2) = 2a con a semiasse orizzontale. I due fuochi abbiano coordinate (-c,0) (c,0). Passando a calcolare l'equazione dell'ellisse con asse corrispondente all'asse delle ascisse avremo:
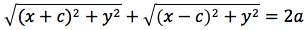
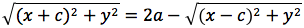
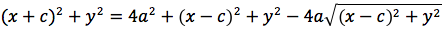
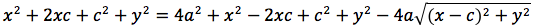
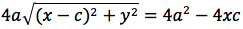
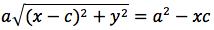
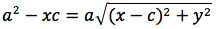
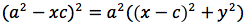
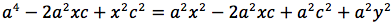
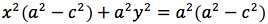
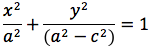
ponendo
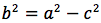
si ottiene infine
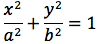
L'ellisse possiede interessanti proprietà di carattere ottico. Infatti, supponiamo di avere un riflettore di forma ellittica. Se si pone una sorgente di luce in uno dei due fuochi, tutti i raggi riflessi passano per l'altro fuoco. Questo ci da inoltre, una spiegazione dei nomi dati a tali punti F, F'. Supponiamo adesso di essere in un ambiente di forma ellittica. Il suono emesso in uno dei due fuochi, anche se molto debole, si sente molto distintamente nell'altro fuoco. Infatti in entrambi i casi, sia le onde luminose che sonore, che sono riflesse dalle pareti percorrono tutte la stessa distanza e giungono contemporaneamente (in fase) all'altro fuoco.
Parabola
Definizione: la parabola è il luogo dei punti del piano le cui distanze da un punto chiamato fuoco e da una retta chiamata direttrice sono uguali.
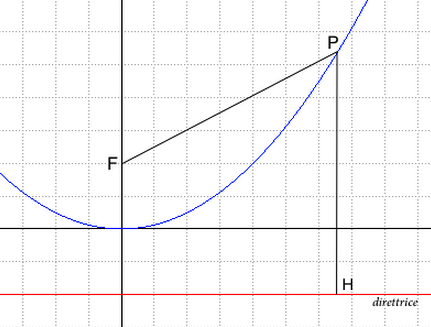
Determiniamo l'equazione di una parabola avente per direttrice una retta orizzontale di equazione y=d e per fuoco il punto F di coordinate (x0,y0). Indichiamo con P(x,y) un punto generico della parabola e imponiamo che la distanza punto fuoco d(P,F) sia uguale alla distanza punto direttrice. Il punto H giacendo sulla stessa verticale deve avere identica ascissa di P quindi H(x,d). Imponiamo quindi la condizione d(P,F)=d(P,H), siccome
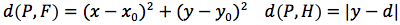
uguagliando d(P;F) e d(P,H) otteniamo
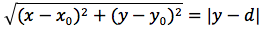
si eleva al quadrato
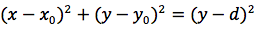
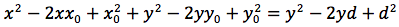
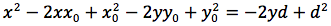
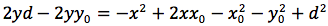
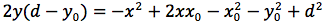
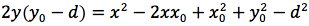
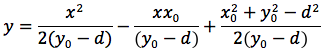
con le seguenti posizioni infine:
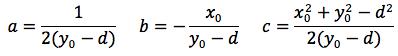
l'equazione della parabola ad asse verticale diventa:
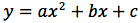
Si noti che, se a risulta positivo, la parabola rivolge la concavità verso l'alto, se a è negativo, la parabola rivolge la concavità verso il basso, inoltre maggiore sarà il valore di a e più stretta risulterà l'apertura della parabola.
Se tutti e tre i parametri a, b, c, sono diversi dallo zero allora si potrà pensare che la parabola di equazione y=ax2+bx+c sia data dalla somma della parabola y=ax2 con la retta y=bx+c. In tal caso, dal punto di vista grafico, la parabola y=ax2+bx+c risulterà traslata nel piano rispetto alla y=ax2, il tipo di traslazione ovviamente dipenderà dai parametri b, c.
In particolare, se b e c sono nulli la parabola ha il vertice corrispondente all'origine del sistema di riferimento. Se a e c sono diversi dallo zero e solo b è nullo la parabola y=ax2+c risulterà sollevata del valore c se c è positivo o abbassata del valore c se c è negativo, rispetto alla parabola di equazione y=ax2.
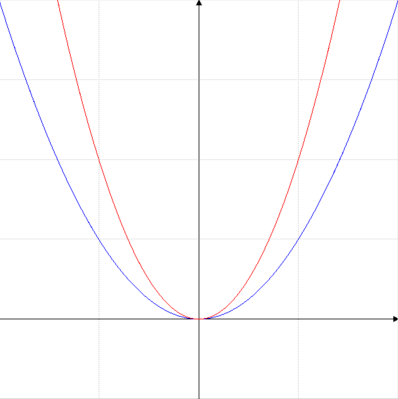
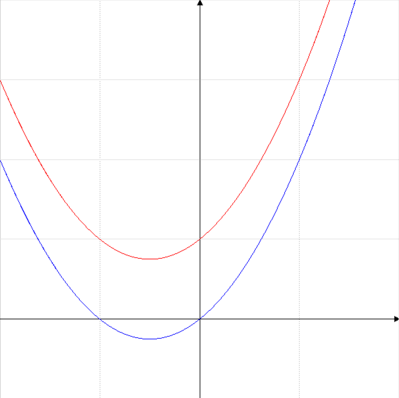
La parabola in rosso y=2x2 è più stretta della parabola y=x2, in blu nella figura, perchè presenta un parametro "a" maggiore
La parabola in rosso y=x2-x+1, risulta sollevata rispetto alla parabola in blu che ha equazione y=x2-x
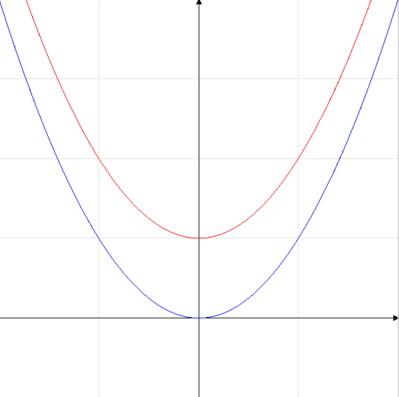
La parabola in rosso y=x2+1 è data dalla somma della retta y=1 e dalla parabola y=x2, in blu nella figura, come si nota la parabola in rosso risulta sollevata rispetto alla parabola in blu
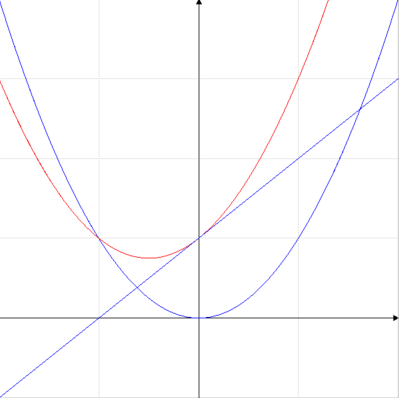
La parabola in rosso y=x2+x+1 è data dalla somma della retta y=x+1 e dalla parabola y=x2, in blu nella figura, come si nota la parabola in rosso risulta traslata rispetto alla parabola in blu
Consideriamo ora, una parabola del tipo y=ax2 ovvero con i parametri b, c uguali a zero. La parabola avrà il vertice nell'origine del sistema di riferimento, il fuoco avrà coordinate F(0,y0) e starà sull'asse delle ordinate, la direttrice avrà equazione y=-y0 in quanto fuoco e direttrice devono essere equidistanti dal vertice. Sia P(x,y) il punto generico della parabola. Imponendo che d(F,P)=d(P,H) dove H è il piede di P sulla direttrice, si ottiene:
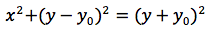
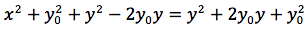
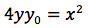
Esplicitando la y
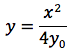
Tenendo presente che la parabola è del tipo: y=ax2, si può dedurre che:
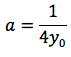
Quindi:
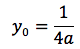
Il fuoco avrà quindi coordinate F(0,1/4a) e la direttrice equazione: y=-1/4a
Consideriamo una parabola che intersechi l'asse delle ascisse in due punti distinti A, B, che abbia quindi il discriminante maggiore di zero. L'asse della parabola passerà per il punto medio del segmento orizzontale AB. L'asse della parabola avrà quindi equazione x=-b/2a. Sostituendo tale valore nell'equazione y=ax2+bx+c, si ottiene l'ordinata del vertice: (-b2+4ac/4a). Se anche la parabola non intersecasse l'asse delle ascisse modificando c si potrebbe abbassare o sollevare la parabola in modo da ciò succeda, ma comunque l'asse della parabola rimarrebbe sempre la stessa e questo è confermato dal fatto che l'ascissa del vertice non dipende dal parametro c, in altre parole le cordinate del vertice sono sempre: V(-b/2a,-Δ/4a). Riassumendo:
La parabola y=ax2 ha vertice V(0,0), fuoco F(0,1/4a), direttrice di equazione: y=-1/4a
La parabola y=ax2+bx+c ha vertice V(-b/2a,-Δ/4a)
Come calcolare fuoco e direttrice della parabola y=ax2+bx+c? Basta tener presente che le due parabole hanno uguale il parametro a e quindi hanno la stessa apertura ovvero una è ottenuta dall'altra tramite una traslazione. In particolare il vertice della prima V(0,0) è traslato nel vertice della seconda V(-b/2a,-b2+4ac/4a). Ogni punto della seconda parabola, rispetto alla prima avrà incrementato l'ascissa di -b/2a e l'ordinata di -b2+4ac/4a. Per ottenere l'ordinata del fuoco della seconda quindi si dovrà incrementare 1/4a di -b2+4ac/4a, quindi il fuoco della seconda sarà: F(-b/2a,(1-Δ)/4a). La direttrice infine avrà equazione y=-(1+Δ)/4a
Iperbole
Definizione: l'iperbole e' il luogo geometrico dei punti del piano per cui e' costante la differenza delle distanze da due punti fissi detti fuochi
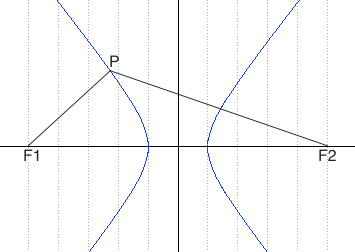
Significa che per tutti i punti P della figura avremo che PF2 - PF1 = costante. Per sapere quanto vale la costante spostiamo il punto P fino a portarlo sull'asse orizzontale, allora si vede che la differenza d(P;F1)-d(P;F2) e' uguale alla distanza fra i due punti dell'iperbole che tagliano l'asse delle x (asse orizzontale). Chiamiamo questa distanza 2a (a per indicare che e' una costante e 2 perche', essendo l'iperbole simmetrica spesso ci servira' la meta' della distanza, cioe' il semiasse orizzontale); quindi avremo per tutte le iperboli d(P;F1)-d(P;F2)=costante=2a con a semiasse orizzontale. I due fuochi abbiano coordinate (-c,0) (c,0). Eseguendo i calcoli determiniamo l'equazione dell'iperbole con asse corrispondente all'asse delle ascisse:
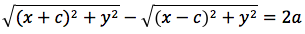
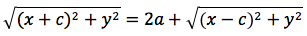
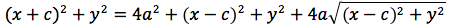
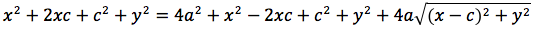
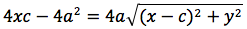
dividendo per 4 si ottiene:
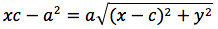
si quadra:
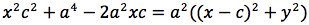
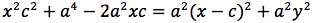
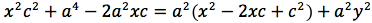
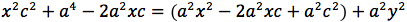
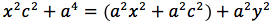
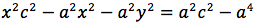
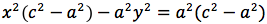
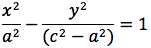
ponendo
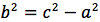
si ottiene infine: