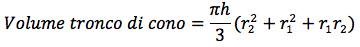Calcolo integrale
Se f(x) è una funzione [a,b]→R continua e positiva ovvero se f(x) ≥ 0, ∀ x ∈ [a,b], si consideri l'area compresa tra questa funzione e le rette y=0, x=a, x=b. Quest'area si chiama trapezoide. Ci proponiamo di dare una definizione di ciò che si intende per area del trapeziode. Dividiamo l'intervallo [a,b] in n intervallini di varia misura indicando con h1, h2 ....hn, le ampiezze di questi intervallini. Prendiamo ad arbitrio nel primo intervallino un punto w1, nel secondo un punto w2, e...nell'ennesimo intervallino un punto wn, e calcoliamo quindi i corrispondenti valori della funzione f(w1), f(w2) ... f(wn). Si arriva così a costruire una famiglia di rettangolini che chiameremo plurirettangolo.
Teorema (enunciato)
Ipotesi: f(x) sia una funzione [a,b]→R continua
Tesi: esiste ed è finito il seguente limite:
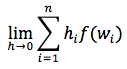
dove h è la massima ampiezza degli intervallini h1, h2 ....hn
Integrale definito
Definizione: si chiama integrale definito della funzione continua f(x): [a,b]→R il numero che rappresenta il limite per h→0 della successione:
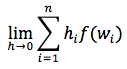
ovvero:
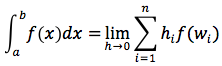
Il valore di questo limite esiste ed ha sempre lo stesso valore comunque si faccia tendere a zero l'ampiezza degli intervallini in cui si suddivide l'intervallo [a,b], e comunque si prendano i punti wi negli intervallini stessi. L'area del trapezoide, per definizione, è proprio uguale al numero determinato da questo limite, hi rappresenta la base e f(wi) l'altezza del singolo rettangolino in cui è suddiviso il trapezoide.
Proprietà dell'integrale definito
1. Se a è minore di b, si pone per definizione
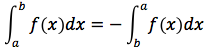
in questo modo si attribuisce un significato all'integrale definito anche quando l'estremo inferiore è maggiore dell'estremo inferiore.
2. Si pone per definizione
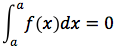
1. Se f(x) è continua in un intervallo [a,c] e b è un valore interno allo stesso intervallo allora
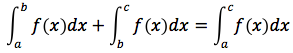
2. Teorema della scomposizione. Se f(x), g(x) .. q(x) sono funzioni continue nell'intervallo [a,b] si ha:
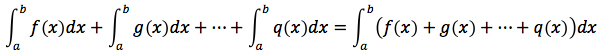
3. Se f(x) è continua in un intervallo [a,c] e k è una costante allora
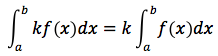
Il teorema della media
Senza dimostrazione.
Ipotesi: sia f(x) una funzione continua definita in un intervallo [a,b].
Tesi: L'integrale definito di f(x) è uguale alla misura dell'intervallo di integrazione [a,b] moltiplicata per il valore che la funzione integranda assume per un opportuno valore w di [a,b].
In altre parole il teorema della media dice che l'area del trapezoide delimitato dalle rette y=0, x=a, x=b e dalla funzione f(x), equivale all'area di un rettangolo che ha per base la stessa base [a,b] e per altezza f(w) dove w è un opportuno valore di [a,b]. La retta orizzontale y=f(w), viene anche detta retta di compenso.
La funzione integrale
Sia f(x) una funzione [a,b]→R continua e positiva f(x) ≥ 0, x ∈ [a,b] L'integrale definito
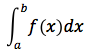
è un preciso numero reale che dipende dagli estremi di integrazione a e b. Supponendo variabile l'estremo superiore che chiameremo x, allora la funzione
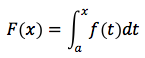
è una funzione dell'estremo superiore x. Come si sarà già notato, per evitare confusione tra la variabile x, della funzione f, e l'estremo superiore x di integrazione, si è sostituito alla variabile x la variabile t. La funzione F(x) si chiama funzione integrale, la f(t) si chiama funzione integranda.
Il teorema fondamentale del calcolo integrale
Ipotesi: Sia f(x) una funzione [a,b]→R continua e positiva f(x) ≥ 0, x ∈[a,b].
Tesi: esiste la derivata della funzione integrale nel punto x ed è uguale al valore che la funzione integranda assume nello stesso punto x, ovvero: F'(x) = f(x).
Dimostrazione: bisogna valutare il limite del rapporto incrementale della funzione integrale per h→0: partiamo dal rapporto incrementale della F:
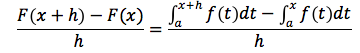
e in base alla proprietà additiva potremo scrivere:
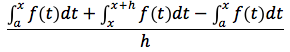
e semplificando:
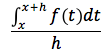
applicando al numeratore il teorema della media, esisterà un w compreso tra [x,x+h] tale che
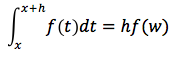
quindi dividendo per h:
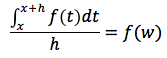
ovvero potremo concludere che il rapporto incrementale della F è uguale a f(w) con w un opportuno valore compreso tra [x,x+h]. Facendo il limite per h tendente a 0, tenendo conto della continuità della f, questo limite sarà uguale a f(x) ovvero:
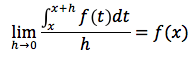
ovvero F'(x)=f(x) che è quanto si voleva dimostrare.
Formula per il calcolo di aree
Supponiamo che P(x) sia una delle primitive di f(x), quindi avremo: P'(x) = f(x) e siccome per il teorema fondamentale si è dimostrato che risulta anche F'(x)=f(x) si può dire che P(x), F(x) differiscono per una costante ovvero: P(x) = F(x) + k ossia:
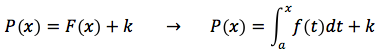
Se si pone x=a risulta:
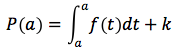
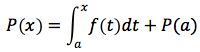
In quest'ultima relazione ponendo x = b e trasportando P(a) al primo membro si ottiene:
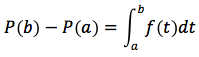
Questa è proprio la formula per il calcolo delle aree e si scrive anche:
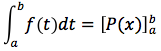
Questa semplice formula permette di superare le difficoltà di calcolare un'area con il limite per h→0 della sommatoria dei plurirettangoli.
Integrale indefinito
Definizione: se P(x) è una funzione che in ogni punto di un intervallo [a,b] abbia per derivata f(x), si dice che P(x) è una primitiva di f(x), ovvero P'(x) = f(x).
La famiglia delle primitive di una funzione f(x) si chiama integrale indefinito della f(x) e si indica con il simbolo:
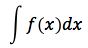
Come si può notare nel simbolo dell'integrale indefinito non sono previsti gli estremi di integrazione. Si parla di "famiglia delle primitive" poiché se p(x) è primitiva di f(x), pure p(x) + k è primitiva di f(x), dove con k si è indicato un qualunque valore reale. Data una funzione e gli estremi di integrazione, l'integrale definito restituisce quindi un numero, che rappresenta un'area. L'integrale indefinito invece data una funzione mi restituisce una famiglia di funzioni ovvero la famiglia delle primitive, in altre parole l'operazione di integrazione indefinita può essere considerata come operazione inversa della derivazione.
Formule fondamentali
Nelle formule scritte di seguito l'integrale si determina in modo immediato ottenendo come primitiva una funzione elementare. Per verificare la validità delle formule è sufficiente derivare la primitiva per ottenere la funzione integranda.
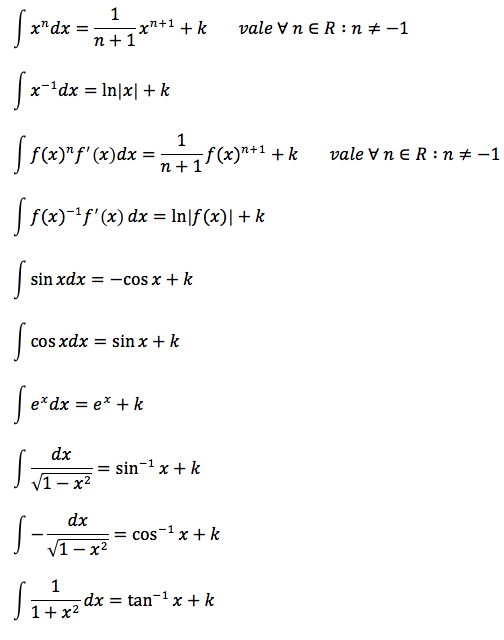
Integrazione per parti
E' una regola che consente, sotto la condizione che la funzione integranda sia scomponibile nel prodotto di due funzioni, di calcolare l’integrale assegnato in termini di un altro integrale. Supponiamo di avere due funzioni f e g derivabili. Applicando la formula della derivata di un prodotto si ottiene:
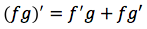
Integrando sia il primo che il secondo termine si ottiene:
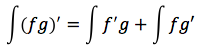
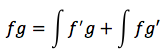
Per ottenere la formula finale:
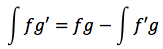
Si possono stabilire due regole generali:
La parte scelta come f' dev'essere facilmente integrabile.
L'integrale che compare al secondo termine dev'essere integrabile più facilmente di quello di partenza.
Integrazione di funzioni razionali
Una funzione razionale è una funzione di questo tipo:
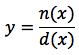
dove n e d sono rispettivamente due polinomi, più precisamente può essere scritta così:
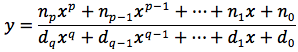
dove ni e di sono rispettivamente i coefficienti del numeratore e del denominatore, p e q rispettivamente i gradi del numeratore e del denominatore.
Se il grado di n(x) è maggiore o uguale al grado di d(x) si esegue la divisione tra numeratore e denominatore. Eseguendo la divisione tra numeratore e denominatore troviamo un quoziente q(x) ed un resto r(x). Il grado del quoziente sarà: grado(q) = grado(n) - grado(d), il grado del resto dovrà essere minore del grado del denominatore d. A questo punto potremo scrivere che n:d=q, con resto r e di conseguenza n=qd+r. Dividendo entrambi i membri dell'ultima relazione scritta per d otteniamo: n/d=(qd+r)/d o anche n/d=q+r/d. In altre parole la nostra funzione razionale può essere scritta come somma del quoziente con l'altra funzione razionale r/d. Tenendo presente che in r/d il grado di r è minore del grado di d. Scrivendo la funzione razionale in questo modo, potremmo scomporre l'integrale in una somma di due integrali:
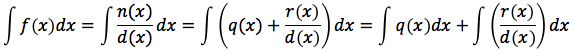
Il primo dei due integrali è immediato in quanto la funzione integranda è un semplice polinomio. Il problema ora diventa quello di calcolare l'integrale di una funzione razionale in cui il grado del denominatore supera il grado del numeratore. Per limitarci a considerare alcuni semplici casi pensiamo che il denominatore sia di secondo grado quindi d(x)=ax2+bx+c e vediamo come procedere nel caso in cui il discriminante sia maggiore di zero oppure sia uguale a zero. Poniamo che il discriminante sia maggiore di zero, l'equazione associata al denominatore avrà due soluzioni distinte x1 e x2, d(x) si potrà così scomporre d(x)=(x-x1)(x-x2) e la funzione da integrare potrà essere scritta:
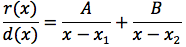
quindi
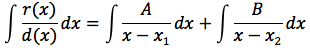
a questo punto impostando un semplice sistema si ricavano A e B e quindi ci si riconduce a risolvere due integrali immediati, si ottiene quindi:
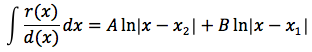
Poniamo che il discriminante sia uguale a zero, l'equazione associata al denominatore avrà una soluzione x0 d(x) si potrà così scomporre d(x)=(x-x1)(x-x1) e la funzione da integrare potrà essere scritta:
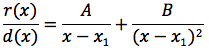
come in precedenza, impostando un semplice sistema si ricavano A e B e quindi ci si riconduce a risolvere due integrali immediati
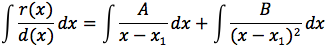
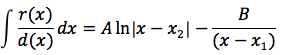
Integrazione per sostituzione
La funzione integranda sia y=f(x), f: A→B, poniamo che F sia una primitiva di f, y=F(x) F: A→B, quindi F'=f. Per rendere il calcolo dell'integrale più semplice, a volte conviene eseguire una sostituzione il che equivale a considerare una funzione x=g(t) g: C→A, il cui codominio sia incluso nel dominio di f. In questo modo si può pensare che la f sia una funzione composta f(g(t)) f: C→B. Essendo anche F definita in A, ha senso considerare anche F come funzione composta ovvero y=F(g(t)).
Per la regola di derivazione delle funzioni composte risulta: (F(g(t)))'=F'(g(t))g'(t) ovvero (F(g(t)))'=f(g(t))g'(t). Esequendo l'integrale sia del primo che del secondo termine della precedente uguaglianza si trova:
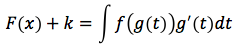
Nel caso in cui si dovesse calcolare l'integrale definito tra x1 e x2, vanno modificati gli estremi di integrazione tenendo presente che la variabile t viene calcolata dalla seguente funzione: t=g-1(x). I nuovi estremi di integrazione saranno t1 e t2 con t1=g-1(x1) e t2=g-1(x2), dunque:
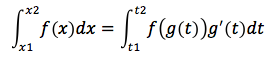
Volume dei solidi di rotazione
Sia f(x) una funzione [a,b]→R continua e positiva ovvero se f(x) ≥ 0, ∀ x ∈ [a,b], si consideri il trapezoide delimitato da questa funzione e le rette y=0, x=a, x=b. Questo trapezoide, ruotando di un giro attorno all'asse x, genera un solido del quale vogliamo definire e calcolare il volume. A questo scopo dividiamo l'intervallo [a,b] in n intervallini di varia misura indicando con h1, h2, ....hn, le ampiezze di questi intervallini. Prendiamo ad arbitrio nel primo intervallino un punto w1, nel secondo un punto w2, e...nell'ennesimo intervallino un punto wn, e calcoliamo quindi i corrispondenti valori della funzione f(w1), f(w2) .. f(wn). Ruotando di un giro completo attorno all'asse x, il plurirettangolo descrive un solido che è l'insieme di n cilindretti aventi per base i cerchi i cui raggi sono i valori f(wi) e per altezza gli intervallini in cui è stato suddiviso [a,b]. Il volume dell'i-esimo cilindretto si calcola quindi πhf2 (wi,) ed il volume del pluricilindro è dato da:
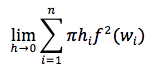
Il volume V del solido di rotazione è quindi dato da:
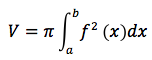
Volume della sfera
Pensiamo che la sfera sia generata dalla rotazione attorno all'asse x del semicerchio avente centro nell'origine e raggio r. L'equazione della circonferenza è: x2+y2= r2 ovvero y2= r2-x2. In base alla formula quindi il volume della sfera è:
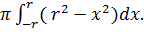
Per rendere i calcoli più semplici potremo, vista la simmetria della sfera calcolare il volume della semisfera:
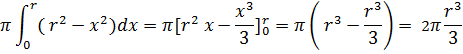
raddoppiando il volume ottenuto troveremo quindi il volume delle sfera:
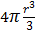
Volume del cono
Il volume del cono di altezza h ottenuto da una rotazione intorno all'asse x della bisettrice y=x si ottiene:
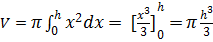
Volume del trono di cono
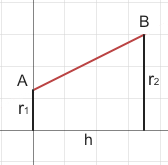
Nella figura di sinistra ruotando intorno all'asse delle ascisse la retta che passa per i punti A(0,r1) e B(h,r2) otteniamo un tronco di cono di altezza h e le basi rispettivamente di raggi r1 e r2. Il coefficiente angolare m, della retta e l'equazione della retta stessa sono indicati nelle figure a destra.
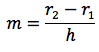
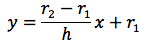
Per ottenere il volume del tronco di cono bisognerà risolvere quindi il seguente integrale:
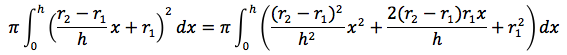
Si ottiene:
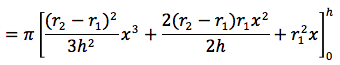
Facendo il minimo comune multiplo si ottiene:
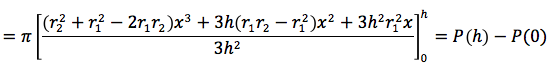
Calcoliamo P(h) e P(0):
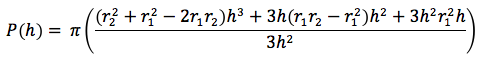
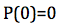
Raccogliendo h, il volume sarà quindi dato da:
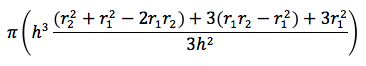
semplificando il denominatore si ottiene:
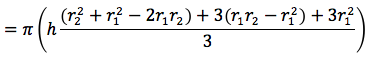
semplificando ulteriormente si ottiene: