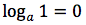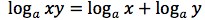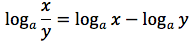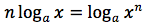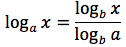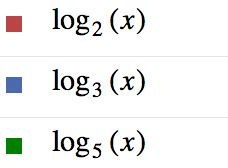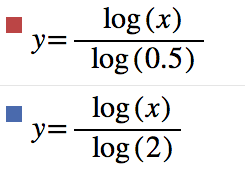Funzioni logaritmiche
La funzione logaritmica è l'inversa della funzione esponenziale. La funzione esponenziale è invertibile se si restringe il codominio a R+. La funzione logaritmo, quindi ha per dominio R+. Non ha senso quindi, calcolare il valore di un logaritmo che ha per argomento un numero negativo.
Definizione: dato un numero positivo a, che chiameremo argomento e un numero b che chiameremo base, il logaritmo in base b di a, è l'esponente che bisogna assegnare alla base per ottenere l'argomento.
Dalla definizione ne consegue quindi che logba=x se e solo se bx=a. Si studiano due casi di funzioni logaritmiche, a seconda che la base assuma un valore compreso tra zero e uno oppure un valore maggiore di uno.
Proprietà del logaritmo
Dimostrazione della prima proprietà
Il logaritmo di uno, in una qualsiasi base, è uguale a zero poichè a0=1.
Dimostrazione della seconda proprietà
si ponga:
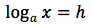
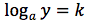
In tal modo per definizione avremo:
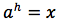
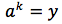
Da cui per le proprietà delle potenze e per definizione di logaritmo:
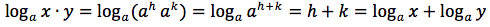
Dimostrazione della terza proprietà
si ponga:
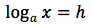
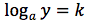
In tal modo per definizione si ha:
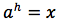
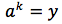
Da cui per le proprietà delle potenze e per definizione di logaritmo:
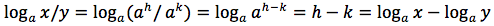
Dimostrazione della quarta proprietà
si ponga:
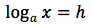
in tal modo si ha:
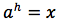
elevando entrambi i membri alla n si ha:
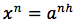
Da cui:
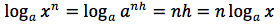
Dimostrazione della quinta proprietà
si ponga:
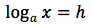
In tal modo per definizione avremo:
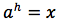
Applicando ad entrambi i termini dell'uguaglianza il logaritmo in base b si ottiene ancora un'uguaglianza:
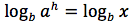
Per la quarta proprietà l'esponente h diventa un fattore per cui si ottiene:
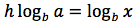
Ricavando h come fosse l'incognita di un'equazione si ottiene:
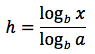
Dato che h è uguale a logaritmo in base a di x, sostituendo si ottiene:
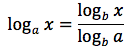
Questa proprietà può essere utile per un cambiamento di base nel calcolo del logaritmo.
Grafici
legenda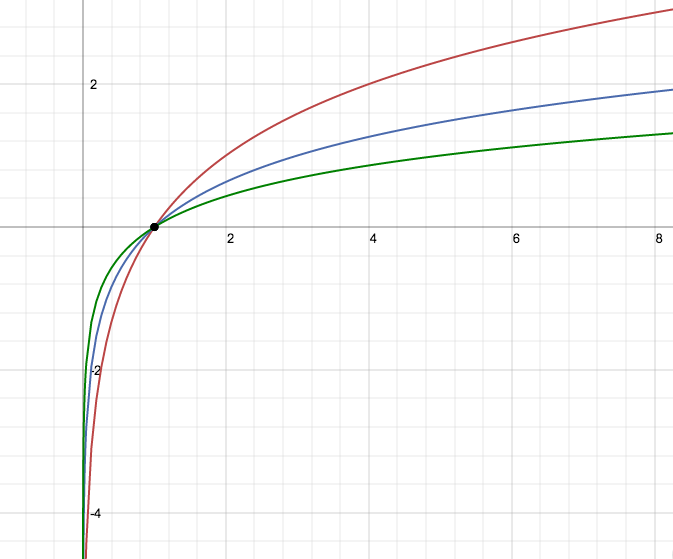
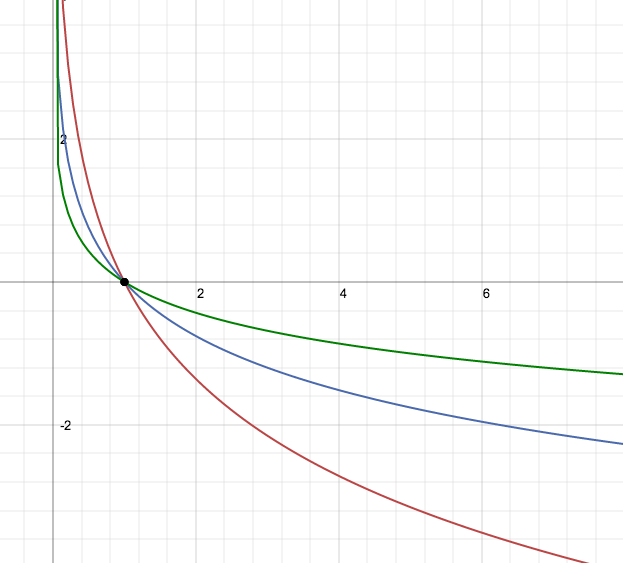
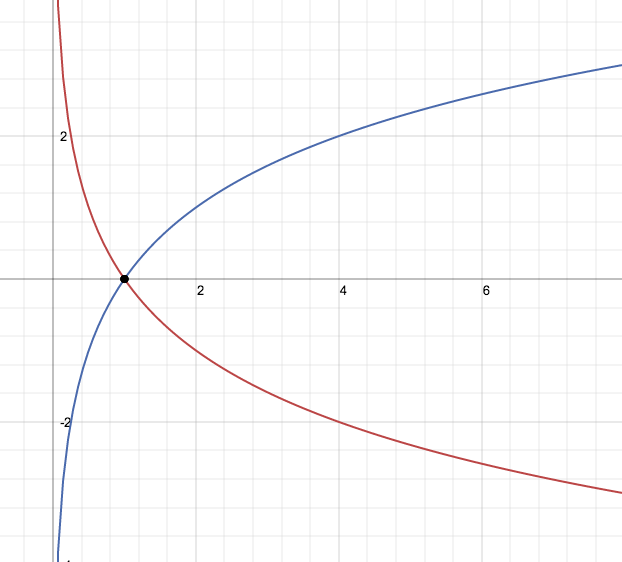
Equazioni logaritmiche
Un'equazione è da considerarsi logaritmica se presenta almeno un logaritmo che abbia l'incognita nel proprio argomento.
Consideriamo equazioni logaritmiche che possano essere scritte nella seguente forma:
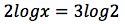
Per la risoluzione di un'equazione logaritmica si procederà per gradi:
Se l'equazione proposta non è del tipo previsto tentare, qualora fosse possibile di trasformarla applicando le proprietà del logaritmo.
Determinare il campo di esistenza delle soluzioni risolvendo il sistema comprendente la disequazioni f(x)>0, g(x)>0 in quanto l'argomento del logaritmo dev'essere strettamente maggiore dello zero.
Cercare le soluzioni dell'equazione f(x)=g(x) dove con f(x) e g(x) indichiamo due funzioni della variabile x.
- Controllare che le soluzioni di quest'ultima equazione ricada entro il campo di esistenza calcolato al punto 2.
Si può anche, senza calcolare il campo di esistenza delle soluzioni, risolvere l'equazione f(x)=g(x) e quindi verificare che le stesse rendano l'argomento del logaritmo maggiore di zero. Un valore, soluzione dell'equazione f(x)=g(x) che non soddisfi a questa condizione non può essere acettato come soluzione dell'equazione logaritmica