Limiti
Sia f una funzione definita in un insieme A, supponiamo che sia continua in un punto x0, di accumulazione per A. Sia fr la restrizione della f all'insieme A - {x0}. Della continuità della f in x0 rimane qualcosa alla fr? I termini nei quali la continuità si esprime non hanno più significato per la fr, la quale non ha alcun valore in x0, però, il fatto che i valori della f per x prossimo ad x0 "sono prossimi" al numero f(x0), che indichiamo con l, può esprimersi anche per la fr: i suoi valori per x prossimo ad x0 (e diverso da x0, e naturalmente x∈ A) "sono prossimi" al numero l.
Spesso accade il contrario: che una funzione f non sia definita in un punto x0 e che la si possa estendere attribuendole in x0 un valore in modo che essa (o meglio la sua estensione) risulti continua in x0. Tale valore evidentemente, dovrà venire desunto dal comportamento della funzione in prossimità di x0. Quindi la funzione f ha come limite l, per x che tende ad x0, e si scrive: limx→x0 f(x) = l , se ponendo f(x0) = l, la funzione risulta continua in x0. Come esempio consideriamo la funzione f(x) = (x-1)(x+3)/(x-1) la quale è definita in R-{1} (Si tratta della retta y=x+3 con un "buco" nel punto x0=1). Ponendo f(1)=4 la funzione prolungata su A U {1} risulta continua. In tal caso il punto 1 è di accumulazione per il dominio della f, ovviamente si ha che il limite esiste ed è: limx→1=4.
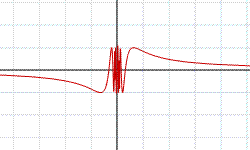
In figura è rappresentata la funzione f(x)=sin(1/x) definita per ogni x eccetto che per x=0. Non è possibile assegnare un valore alla f nel punto 0 in modo da renderla continua perché in ogni intorno di 0 la f assume tutti i valori dell'intervallo {y: -1≤y≤1 }, mentre per raggiungere il nostro scopo, al restringersi della variabilità di x intorno a 0 i valori della f dovrebbero restringersi intorno ad un numero l. Attraverso questo esempio si può notare che non sempre una funzione si comporta, in prossimità di un punto x0 , così come la restrizione fr di una funzione che in x0 sia continua. In questo caso il limite per x tendente a 0 non esiste.
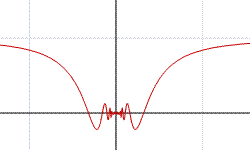
Per quanto riguarda invece la funzione f(x) = xsin(1/x) in figura che è definita in A=R-{0} , con 0 punto di accumulazione per A, si ha: limx→0 xsin(1/x) = 0. Ponendo f(0)=0 la funzione prolungata su tutto R risulta continua.
Definizione di limite
Si dice che una funzione f, definita in A, ha come limite il numero l al tendere di x verso x0 (punto di accumulazione di A) se: per ogni intorno U di l, esiste un intorno V di x0, tale che, per ogni x di A appartenente a V-{x0} ne consegue che f(x) appartiene a U.
In simboli:
1. ∀ U(l), ∃ V(x0): ∀ x ∈ V-x0, (x∈A) ⇒ f(x) ∈ U.
Oppure, che è lo stesso:
2. ∀ U(l), ∃V(x0): ∀ x ∈ V-{x0} (x∈A) ⇒ f(x) ∈ U, con U e V intorni centrati di raggio δ e ε.
Oppure, che è lo stesso:
3. ∀ ε > 0, ∃δ >0: ∀ x: ׀x-x0 ׀ < δ (x∈A) ⇒ ׀f(x) - l׀ < ε.
Oppure, che è lo stesso:
4. ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x) - l׀ < ε
Per memorizzare la definizione
Teniamo presente che la definizione può essere suddivisa in quattro parti. Di definizioni ne sono scritte quattro, ma tutte tra di loro equivalenti, infatti i cambiamenti riguardano solo i riferimenti. La 1. fa riferimento agli intorni, la 2. agli intorni centrati, la 3. ai raggi degli intorni centrati, la 4. ha riferimenti misti, ovvero la prima e la quarta parte riportano i raggi, la seconda e la terza parte gli intorni. In ogni caso, la prima e la quarta parte interessano l'asse delle y, la seconda e la terza l'asse x. La 1. è sicuramente la più "intuitiva", la 2. è del tutto analoga, la 3. costituisce una sorta di passaggio di consegne tra gli intorni centrati e i raggi degli stessi, la 4. viene utilizzata nei calcoli, per esempio, per la verifica di un limite.
| Prima parte | Seconda parte | Terza parte | Quarta parte |
| ∀ U(l), | ∃ V(x0): | ∀ x ∈ V-x0, (x∈A), | ⇒ f(x) ∈ U |
| ∀ U( di centro l), | ∃ V( di centro x0): | ∀ x ∈ V-x0, (x∈A), | ⇒ f(x) ∈ U |
| ∀ ε > 0, | ∃ δ > 0: | ∀ x: ׀x-x0׀ < δ (x∈A), | ⇒ ׀f(x) - l׀ < ε |
| ∀ ε > 0, | ∃ V(x0): | ∀ x ∈ V-x0, (x∈A), | ⇒ ׀f(x) - l׀ < ε |
L'essere f continua in x0 (punto di accumulazione per A) equivale ad essere: limx→x0 f(x) = f(x0) ed infatti enunciare la definizione di continuità equivale ad enunciare la definizione di limite con f(x0) al posto di l.
Limite infinito, limite per x→∞ .
Non possiamo pensare di trattare +∞, -∞ come due qualsiasi altri numeri pensando che +∞ segua tutti i punti di R e -∞ li preceda tutti, anche se ciò potrebbe dare dei vantaggi dal punto di vista della struttura d'ordine. Dal punto di vista algebrico però, ogni tentativo di estendere ai nuovi enti l'addizione e la moltiplicazione porterebbe a far cadere qualcuna delle proprietà formali, si pensi di dar significato per esempio al seguente prodotto: 0(+∞), oppure alla seguente somma:(+∞) + (-∞). Allora rinunciamo ad aggiungere +∞,-∞ all'insieme dei numeri reali, ma continuiamo a chiamare intorno di +∞ ogni intervallo del tipo {x: x>a}. Per i numeri l'assenza di un segno preposto sottointende che sono positivi, per il caso dell'infinito la convenzione di scrittura è diversa per cui intorno di ∞ è ogni insieme del tipo {x: lxl>a}; ∞ è di accumulazione per A se ogni intorno di ∞ contiene punti di A. A questo punto, risulterà naturale estendere la definizione di limite anche quando in luogo di x0 oppure di l vi sia uno dei simboli +∞, -∞, ∞.
Per esempio limx→x0 f(x) = -∞ (presupposto che x0 sia di accumulazione per A) significa che: per ogni intorno U di -∞ , esiste un intorno V di x0, tale che, per ogni x appartenente a V-{x0} ne consegue che f(x) appartiene a U.
In simboli:
∀U(-∞), ∃ V(x0): x ∈ V-{x0}, (x∈A) f(x) ∈ U. O che è lo stesso
∀U(-∞), ∃V(x0): ∀ x ∈ V-{x0}, (x∈A) ⇒ f(x) ∈ U, con V intorno centrato di raggio δ. O che è lo stesso:
∀ k, ∃δ >0: x: ׀x-x0׀ < δ, (x∈A) ⇒ f(x)<k. O che è lo stesso:
∀ k, ∃ V(x0): x ∈ V-x0, (x∈A) ⇒ f(x) < k.
Vediamo un altro esempio: limx→-∞ f(x) = +∞ significa che:
per ogni intorno U di +∞ , esiste un intorno V di -∞, tale che, per ogni x appartenente a V ne consegue che f(x) appartiene a U
in simboli:
∀U(+∞ ), ∃ V(-∞): x ∈ V, (x∈A) ⇒ f(x) ∈ U.
O che è lo stesso: ∀ k, ∃ h: x: x < h, (x∈A) ⇒ f(x) > k.
O che è lo stesso:
∀ k, ∃ V(x0): x ∈ V, (x∈A) ⇒ f(x) > k
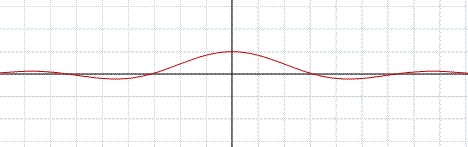
Nel caso in cui si parli di intorni di +∞ oppure -∞ il concetto di intorno centrato viene a perdersi. Nella funzione sinx/x (nella figura di sotto) valgono i seguenti limiti: limx→+∞sinx/x=0, limx→-∞sinx/x=0, ciò si può esprimere scrivendo limx →∞ sinx/x =0, ovvero questo limite congloba i due precedenti.
Si noti quindi che
l'essere: limx→+∞ f(x)= l,
limx→-∞ f(x)= l
( l finito o no) equivale all'essere: limx→∞
f(x)= l, e
questo significa che:
∀ ε >
0, ∃ k: ∀x: lxl>k, ⇒ lf(x)-ll<ε
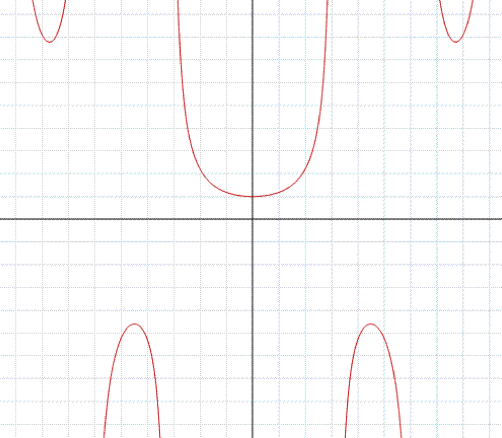
Allo stesso modo come si è provato che, per x→x0, f(x) non può avere due limiti finiti distinti, è facile provare che, per x→x0 (oppure +∞, -∞ in luogo di x0), f(x) non può avere un limite finito e un limite infinito, né può tendere simultaneamente a +∞ oppure -∞. Dall'essere limx→x0 f(x) = ∞, non segue che il limite stesso possa precisarsi con +∞ oppure -∞. . Nella figura di sotto è rappresentata la funzione x/sinx che è la reciproca della precedente. È: limx→ +∞ x/sinx= ∞, questo perché lx/sinx l≥lxl, ma la funzione, non tende a +∞ 0-∞. L'affermazione limx →+∞f(x)=∞ significa che: per ogni numero reale h, esiste un numero reale k tale che per x>k si abbia ׀f(x)׀>h, in simboli:
∀ h ∈ R, ∃ k ∈ R: se x > k → ׀f(x)׀>h
A volte interessa il comportamento di una funzione a sinistra o a destra di x0, ossia il comportamento per x tendente a x0 delle restrizioni della f agli insiemi {x: x<x0} e {x: x>x0} sempre che x appartenga ad A e x0 sia di accumulazione per i due insiemi. Se la restrizione a sinistra ammette limite l per x→ x0 esso si dice limite sinistro della f per x→ x0 e si esprime scrivendo: limx→xo- f(x)= l. Analogamente si esprime il limite destro. L'esistenza del limite per x→x0 della f(x) se x0 è di accumulazione per entrambi gli insiemi considerati, equivale al fatto che il limite destro ed il limite sinistro sono entrambi corrispondenti ad l.
Calcolo del limite
Per il calcolo del limite ci saranno utili seguenti teoremi:
Teorema 1 Il limite di una somma di funzioni e' uguale alla somma dei limiti.
Teorema 2 Il limite di un prodotto di funzioni e' uguale al prodotto dei limiti.
Teorema 3 Il limite di un rapporto di funzioni e' uguale al rapporto dei dei limiti.
Dimostriamo il teorema 1
Ipotesi: Siano f, g funzioni definite su un certo dominio A, escluso al più un punto x0 che sia punto di accumulazione per A. Valgano inoltre i seguenti limiti: limx→x0 f(x)=l limx→x0 g(x)=m. Si intende che i limiti indicati con le lettere l, m, assumono valori reali finiti.
Tesi: limx→x0 f(x)+g(x)=l+m
Dimostrazione: Per la definizione di limite avremo:
∀ ε' > 0, ∃ V'(x0): ∀ x ∈ V'-x0, (x∈A), ⇒ ׀f(x) - l׀ < ε'
∀ ε'' > 0, ∃ V''(x0): ∀ x ∈ V''-x0, (x∈A), ⇒ ׀g(x) - m׀ < ε''
Bisogna dimostrare che vale la seguente definizione:
∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)+g(x) - l - m׀ < ε
tenendo presente che per la proprietà dei valori assoluti si ha che: ׀f(x)+g(x) - l - m׀ > ׀f(x) - l׀ + ׀g(x) - m׀ e che quest'ultima espressione risulta < ε'+ε'' basta prendere ε ≥ ε'+ε'' per la proprietà transitiva della disuguaglianza la definizione del limite della funzione somma risulta essere soddisfatta.
La dimostrazione degli altri due teoremi risulta essere pressochè analoga e sfrutta ancora la definizione di limite. Da questi teoremi, si possono trarre delle regole che facilitano il calcolo del limite.
La prima regola è sostituire il valore a cui tende la variabile x nell'espressione analitica della funzione stessa. Ma cosa succede quando i due limiti non sono finiti? Per esempio può, presentarsi il caso in cui il limite della funzione f sia finito e quello della funzione g +∞, in tal caso il limite della funzione somma è +∞. Nelle tabelle sono presentati tutti i casi che si verificano.
| lim f | lim g | lim f+g |
| l | m | l+m |
| l | +∞ | +∞ |
| l | -∞ | -∞ |
| +∞ | +∞ | +∞ |
| -∞ | -∞ | -∞ |
| +∞ | -∞ | ind |
| lim f | lim g | lim f*g |
| l | m | l*m |
| +∞ | +∞ | +∞ |
| +∞ | -∞ | -∞ |
| -∞ | -∞ | +∞ |
| l | ∞ | ∞ |
| ∞ | 0 | ind |
| lim f | lim g | lim f/g |
| l | m | l/m |
| l | ∞ | 0 |
| ∞ | l | ∞ |
| l | 0 | ∞ |
| ∞ | ∞ | ind |
| 0 | 0 | ind |
Si può notare che la funzione somma ha il caso indeterminato +∞-∞, la funzione prodotto il caso 0*∞, la funzione rapporto ha due casi indeterminati 0/0 ed ∞/∞. In tali casi non ci sono teoremi che permettono di stabilire il limite a priori, ma, caso per caso, sono necessarie ulteriori analisi per eseguire il calcolo. Nella sezione esercitazioni sono presenti alcuni esercizi guida che presentano le tecniche più comuni per risolvere i casi indeterminati.
Teoremi sui limiti
Nelle seguenti righe, facendo sempre riferimento alla definizione di limite, si dimostano tre importanti teoremi.
Teorema dell'unicità del limite
Ipotesi: Sia f una funzione definita su un certo dominio A, escluso al più un punto x0 che sia punto di accumulazione per A. Valga inoltre il seguente limite: limx→x0 f(x)=l
Tesi: il limite è unico.
Nota: La dimostrazione di questo teorema è particolare in quanto è una dimostrazione per assurdo. Tale dimostrazione sfrutta l'equivalenza delle due tipologie dimostrative:
1. diretta: ipotesi → tesi
2. per assurdo: non tesi → non ipotesi
La dimostrazione in generale più usata è quella diretta, però, questo teorema conviene dimostrarlo partendo dalla non tesi, arrivando, attraverso la dimostrazione, alla non ipotesi.
Dimostrazione:
Partire dalla non tesi significa quindi ammettere l'esistenza di due limiti diversi l, l' per x → x0 ovvero:
limx→x0 f(x)=l
limx→x0 f(x)=l'
Per come sono stati scritti i due limiti supponiamo, per ora, che sia il valore x0 che il valore l siano finiti. Per la definizione di limite avremo contemporaneamente:
∀ U(l), ∃ V(x0): ∀ x ∈ V-x0, (x∈A) ⇒ f(x) ∈ U
∀ U'(l), ∃ V'(x0): ∀ x ∈ V '-x0, (x∈A) ⇒ f(x) ∈ U'
U ed U' possiamo pensarli disgiunti ovvero U∩U'=∅ e in V ∩ V', che è ancora un intorno di x0 le definizioni scritte devono valere contemporaneamente. Per tanto succede che prendendo un valore x appartenente a V ∩ V' la relativa f(x) deve cadere contemporaneamente sia in U che in U'. Ad un valore del dominio corrisponderebbero due nell'insieme immagine quindi la f non sarebbe più una funzione e ciò va contro l'ipotesi. A questo punto è stato dimostrato il teorema non tesi → non ipotesi che è equivalente al teorema ipotesi → tesi. Il limite è quindi unico. Analogamente si può dimostrare il teorema nel caso in cui il valore del limite ed il valore a cui tende x siano uno finito ed uno infinito oppure entrambi i valori siano infiniti.
Teorema del confronto (detto anche teorema dei due carabinieri)
Ipotesi:
Siano f, g, h, tre funzioni definite sullo stesso dominio A, escluso al più un punto x0 che sia punto di accumulazione per A.
Per ogni x appartenente ad A si abbia f(x) ≤ g(x) ≤ h(x).
Valgano inoltre i seguenti limiti: limx→x0 f(x)=l, limx→x0 h(x)=l
Tesi: limx→x0 g(x)=l
Dimostrazione:
Per la definizione di limite applicata alla f si ha che: ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)- l׀ <ε
Per la definizione di limite applicata alla h si ha che: ∀ ε > 0, ∃ V'(x0): ∀ x ∈ V'-x0, (x∈A), ⇒ ׀h(x)- l׀ <ε
In V ∩ V', che è ancora intorno di x0, valgono contemporaneamente sia ׀f(x)- l׀ <ε che ׀h(x)- l׀ <ε
queste ultime due relazioni, che sono disequazioni con valori assoluti, sono equivalenti a:
l-ε <f(x) <l+ε e rispettivamente a:
l-ε <h(x) < l+ε
Tenendo quindi conto anche delle ipotesi, in V ∩ V' si avrà l-ε < f(x) ≤ g(x) ≤ h(x) < l+ε
quindi l-ε < g(x) < l+ε o che è lo stesso: ׀g(x)- l׀ <ε
Quindi si è dimostrato che ∀ ε > 0, ∃ V ∩ V'(x0): ∀ x ∈ V ∩ V'-x0,(x∈A), ⇒ ׀g(x)- l׀ <ε
Ciò vuol dire, in base alla definizione di limite che:
limx→x0 g(x)=l.
Il nome del teorema, ricorda quindi che la funzione g deve confrontarsi con le f e h ovvero, le funzioni f e h rappresentano i due carabinieri che costringono la g a fare lo stesso loro percorso che, presumibilmente, finirà in galera.
Teorema della permanenza del segno
Ipotesi:
Sia f(x) una funzione definita in un dominio A escluso al più un punto x0 che sia punto di accumulazione per A.
Valga il seguente limite: limx→x0 f(x)=l
Tesi:
Esiste un intorno di x0, escluso x0 stesso, in cui la funzione assume lo stesso segno di l.
Dimostrazione:
Supponiamo che l sia positivo, per definizione si ha che: ∀ ε > 0, ∃ V(x0): ∀ x ∈ V-x0, (x∈A), ⇒ ׀f(x)- l׀ <ε, scegliamo ε=l/2, avremo quindi che ׀f(x)- l׀ <l/2, sviluppando il valore assoluto si trova che: l-l/2<f(x)<l+l/2 ovvero l/2<f(x)<3l/2. Si è così dimostrato che esiste un intorno di x0, in cui la funzione assume valori positivi. Analogamente si può dimostare che il teorema vale anche nel caso in cui il limite assume valore negativo.
Limiti notevoli
Limx→0 sinx/x=1 (con x espresso in radianti)Il limite si presenta nella forma forma indeterminata del tipo 0/0. Bisogna valutare il comportamento della funzione sinx/x in un intorno dello zero e questo ci permette di considerare l'angolo x < π/2.
Pensando alla misura di senx e tanx possiamo scrivere che:
1. sinx<x<tanx
dove x rappresenta la lunghezza dell'arco sotteso dall'angolo x. La misura in radianti dell'angolo al centro che insiste sull'arco è x così come è x la misura dell'arco nell'unità di misura della lunghezza.
A questo punto consideriamo due casi facendo vedere che:
caso a. Limx→0+ sinx/x=1
caso b. Limx→0- sinx/x=1.
Caso a
essendo sinx >0, dividendo ciascun termine per sinx non si altera il verso della 1. ottenendo:
1<x/sinx<1/cosx
quindi si passa ai reciproci invertendo il verso:
cosx<sinx/x<1
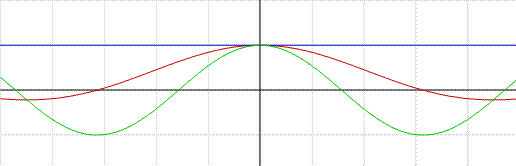
ed essendo Limx→0+ cosx=1 Limx→0+ 1=1 si può applicare il teorema del confronto poichè, come si nota anche in figura, la funzione sinx/x è compresa tra la funzione y=cosx e la funzione costante y=1. Si ottiene: Limx→0+ sinx/x=1
Caso b
essendo sinx <0, dividendo ciascun termine per sinx si inverte il verso della disuguaglianza e si ottiene:
1>x/sinx>1/cosx
osservando che a sinistra dello zero sinx<0, x<0 e cosx>0 passando ai reciproci si ottiene: 1>sinx/x>cosx
ed essendo Limx→0- cosx=1 si può applicare il teorema del confronto poichè, come nel primo caso, anche in un intorno dello zero, la funzione sinx/x è compresa tra la funzione y=cosx e la funzione costante y=1. Quindi, siccome: Limx→0+ sinx/x=1 poiché Limx→0- sinx/x=1 allora Limx→0 sinx/x=1 C.V.D.
Se si misurano gli angoli in gradi la disuguaglianza sinx<x<tanx deve essere sostituita dalla sinx<xπ/180<tanx come si ricava tenendo conto del legame tra la misura in gradi e in radianti di uno stesso angolo.
Da qui segue che: Limx→0 sinx/x=π/180
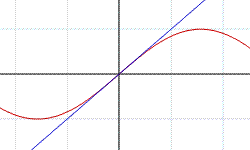
Supponiamo che l’unità di misura degli angoli sia il radiante. Se sulla circonferenza goniometrica, che ha raggio uguale ad uno, prendiamo un arco di lunghezza pari a 1 allora, l’angolo che insiste su questo arco misura 1 radiante. Per definizione, infatti, il radiante è l’angolo al centro della circonferenza che sottende un arco di lunghezza pari al raggio. Più in generale, se sulla circonferenza goniometrica prendiamo un arco di lunghezza x allora l’angolo che insiste su questo arco avrà un’ampiezza di x radianti. Se il raggio della circonferenza goniometrica è uguale a 1 (per esempio 1cm) una sinusoide completa corrisponde a 2π (~6,28cm) sull'asse x. Dire che il limite per x tendente a zero del rapporto sinx/x vale uno, dal punto di vista grafico significa che la funzione y=x risulta essere tangente alla funzione sinx nell’origine, come si può notare in figura.
Diverse considerazioni vanno fatte nel caso in cui l’unità di misura sia il grado. In questo caso, considerato sempre che il raggio della circonferenza goniometrica è uguale a 1 (per esempio 1cm), ad un angolo giro corrisponde 360 (3,60m) sull'asse x, in altre parole, usando un linguaggio descrittivo, potremo dire che, il grafico della funzione seno, formerà una sinusoide piuttosto allungata. Si tenga presente che 1 grado corrisponde a π/180 (~0,01745) radianti. In questo caso la retta tangente alla funzione sinx sarà una retta passante comunque per l'origine, ma con un coefficiente angolare molto inferiore ad uno, ovvero la retta y= (π/180)x. Il limite per x tendente a zero del rapporto sinx/x è infatti π/180. In tutte le osservazioni di carattere grafico fatte, si è che usata, per il sistema di riferimento, la scala 1:1. Bisogna fare attenzione a non confondere il limite notevole appena dimostrato con il seguente: Limx→∞ sinx/x.

In questo caso x non tende a zero bensì a infinito e la forma non è indeterminata essendo espressa da un rapporto tra una funzione limitata e una funzione che tende ad infinito. Si noti quindi che questo limite è uguale a zero. Si veda il grafico della funzione sinx/x in figura.
Teorema: limx→∞ (1+1/x)x = êSi dimostra, ma omettiamo la dimostrazione, che questo limite esiste ed è un valore compreso tra 2 e 3, si indica con il simbolo ê si chiama il numero di Nepero ed è un numero irrazionale che, scritto in notazione decimale, approssimato per difetto alla dodicesima cifra dopo la virgola è: 2,718281828459. In figura il grafico della funzione (1+1/x)x che, come si nota, ha per asintoto orizzontale la retta y=ê.
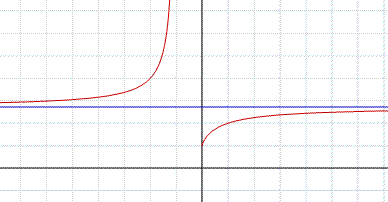
Il numero di Nepero entra in molti fenomeni naturali (per esempio la catenaria) e si assume come base nei logaritmi poiché le formule in cui intervengono i logaritmi in questa base, si presentano sotto un aspetto semplice.
| Ai | modesti | e | vanitosi | ai | violenti | e | timorosi | do | cantando | gaio | ritmo | logaritmo |
| La | sangria | è | squisita | da | ebbrezza | e | allegria | la | quantità | però | resti | contenuta |
| Lo | zampone | è | modenese | il | gianduia | è | torinese | le | tortelle | sono | tutte | bolognesi |
| La | bambina | è | affamata | la | minestra | è | squisita | la | scodella | vien | tosto | terminata |
| Io | ricordo | a | menadito | la | costante | e | mediante | la | tiritera | data | quale | riepilogo |
| 2 | 7 | 1 | 8 | 2 | 8 | 1 | 8 | 2 | 8 | 4 | 5 | 9 |
alcune poesie .... per ricordare a memoria le prime 13 cifre del numero di Nepero, la quattordicesima è lo zero.