Grafici a tratti
- Classi
terze
- Durata
6 ore
- Scopo
Realizzare un'applicazione con il foglio elettronico che permetta di descrivere una funzione e di ottenere il suo grafico in un intervallo dell'asse X.
- Prerequisiti
Indirizzamenti assoluti e relativi, uso dei grafici a dispersione.
Introduzione
Questa esercitazione è la base per moltissime altre che prevedono l'utilizzo di grafici per svariati scopi; è importante quindi capire chiaramente i vari passaggi che portano alla realizzazione della procedura perché la stessa ricorrerà spesso in altre situazioni.
La nostra funzione può essere definita attraverso i suoi coefficienti; la procedura vale per funzioni di qualsiasi grado ma il grado massimo deve essere definito al momento della creazione del foglio.
Se definiamo come 2 il grado massimo della nostra funzione, la stessa si presenterà così:
f(x) = ax2 + bx + c
dove a, b e c sono chiamati coefficienti e sono rappresentati da numero reali a caratterizzare la specifica funzione; naturalmente, azzerando il coefficiente a si può ottenere una funzione di grado inferiore; quindi la costruzione definisce il grado massimo della funzione mentre quello minimo è 1.
Ma come si passa dalla definizione della funzione al suo grafico ? è necessario individuare una serie di punti in coordinate X e Y che appartengono alla funzione un po' come si fa su un foglio di carta millimetrata con la calcolatrice.
Quanti punti ? dipendono dalla complessità della funzione, ma poichè non saremo noi a dover fare i calcoli è opportuno definire un numero elevato di punti (per esempio 1000) che comunque andrà definito nella fase di costruzione del foglio. In generale, maggiore è il numero di punti maggiore sarà la definizione grafica della funzione.
Un altro aspetto da tenere in considerazione è che il grafico della funzione si applica all'asse X che è infinito; naturalmente sul foglio elettronico dobbiamo definire dei valori di intervallo finito, da X1 a Xn , nel quale rappresentare il grafico; questi valori dovranno essere variabili perchè non possiamo sapere a priori in quale porzione dell'asse X osservare il nostro grafico in modo da avere un risultato "interessante".
Dalla teoria alla pratica
Utilizzando il foglio elettronico per questo esercizio, un aspetto da non trascurare è la scrittura della funzione; l'equazione deve essere descritta attraverso i coefficienti a,b e c ma la loro presentazione può rendere semplice o complicata l'interpretazione della funzione stessa da parte dell'utilizzatore che, rammentiamolo, spesso non è colui che ha scritto il foglio elettronico.
Una soluzione semplice ed efficace per inserire e proporre la funzione può essere quella indicata di seguito:
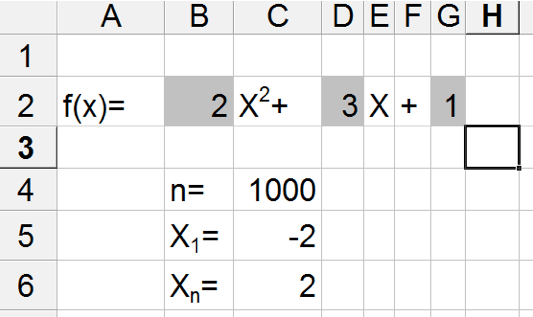
Come si può notare le celle con sfondo grigio sono quelle dove vanno inseriti i coefficienti che permettono di descrivere una qualsiasi funzione (nell'esempio riportato in figura il grado massimo è 2); nel contempo la funzione è perfettamente riconoscibile come tale.
Inoltre è stato definito il numero di punti (valore n=1000) e l'intervallo dell'asse X nel quale rappresentare la funzione (valore iniziale X1 =-2; valore finale Xn =+2);
Ora non ci resta che definire i 1000 punti sull'asse X dai quali ricavare le corrispondenti coordinate Y. Ma come procedere per definire i punti ?
il modo più semplice è individuare i punti uniformemente distribuiti lungo il segmento compreso fra le coordinate X1 ed Xn sull'asse X. Ma qual è la distanza costante fra questi punti ?
Ci può aiutare una semplice osservazione. Se consideriamo un segmento S su cui vogliamo individuare 3 punti equidistanti otterremo una distribuzione dei punti come in figura
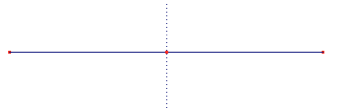
la distanza fra i punti, in questo caso, è pari alla metà della lunghezza del segmento:
distanza fra i 3 punti = lunghezza S / 2
nel caso volessimo ottenere 4 punti sullo stesso segmento, avremmo la situazione come da figura seguente

la distanza fra i punti, in questo caso, è pari ad un terzo della lunghezza del segmento:
distanza fra 4 punti = lunghezza S / 3
in generale se vogliamo individuare la distanza fra n punti equidistanti su un segmento la formula sarà:
distanza fra n punti = lunghezza S / (n -1) applicando questa formula al nostro foglio, l'intervallo fra i nostri punti sull'asse X sarà:
lunghezza del segmento / (n - 1)
nello specifico, dato che la lunghezza di un segmento sull'asse X è pari alla differenza fra le coordinate X, otterremo:
intervallo fra i punti = (Xn - X1 )/(n-1)
Come applicare questa osservazione al nostro sistema ?
La prima coordinata X è pari al valore di X1
La seconda coordinata X sarà pari al valore della coordinata X1 + l'intervallo trovato in precedenza
La terza coordinata X sarà pari al valore della coordinata X2 + l'intervallo
La quarta coordinata X sarà pari al valore della coordinata X3 + l'intervallo
E così via.
Quindi il valore successivo della coordinata X si troverà a partire dal valore precedente incrementato dell'intervallo. Se la formula "base" verrà impostata correttamente, utilizzando in modo opportuno indirizzamenti assoluti e relativi, sarà sufficiente copiarla per 999 righe fino ad arrivare al 1000-simo valore delle X; per capire se l'operazione è stata svolta correttamente, l'ultimo valore dovrà assumere un valore pari a quello impostato per Xn.
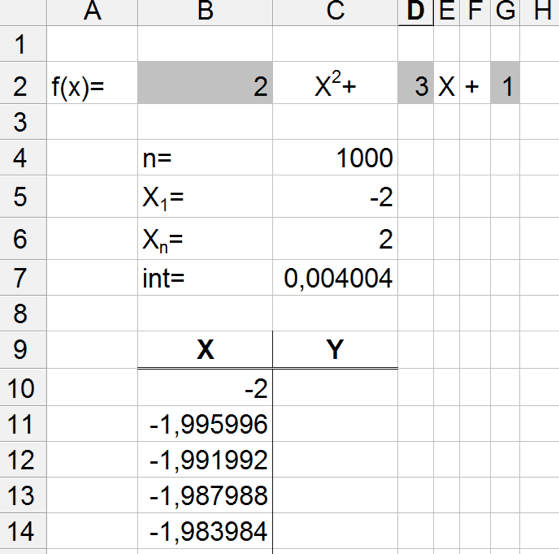
Il calcolo dei valori della Y è piuttosto semplice, essendo noti i coefficienti che descrivono la funzione ed i valori della X corrispondenti. Anche in questo caso, usando opportunamente indirizzamenti assoluti e relativi e costruendo correttamente la formula base, sarà sufficiente "trascinarla" sulle righe sottostanti per 999 volte.
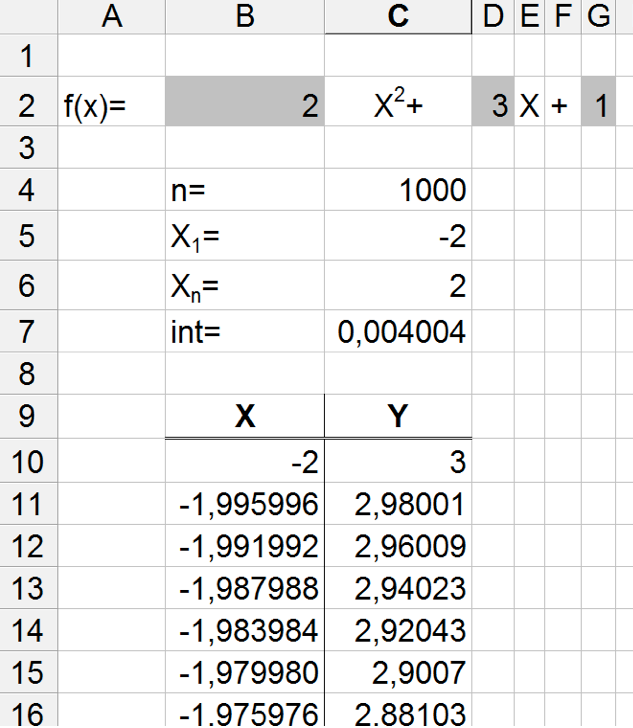
Ora abbiamo una sequenza di coordinate di punti sul piano cartesiano che appartengono alla funzione definita. Selezionando tutti i valori della X ed i valori della Y possiamo procedere all'autocomposizione del grafico: è molto importante utilizzare, come tipo di grafico, la "dispersione XY" che mette in relazione i valori X con i valori Y; utilizzando altri tipi di grafici si potrà ottenere forse un risultato simile ma l'asse delle X apparirà scorretto perché enumererà i punti a 1 a 1000 anzichè assumere i valori previsti per la X. Anche la scelta del tratto per il grafico è molto importante è dovrà orientarsi verso le linee smussate e senza punti.
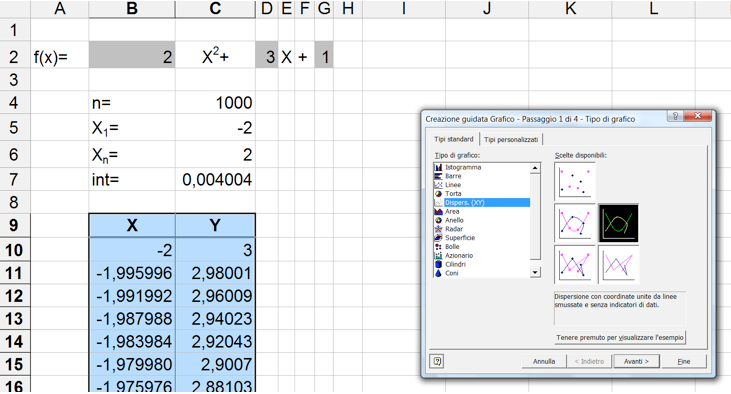
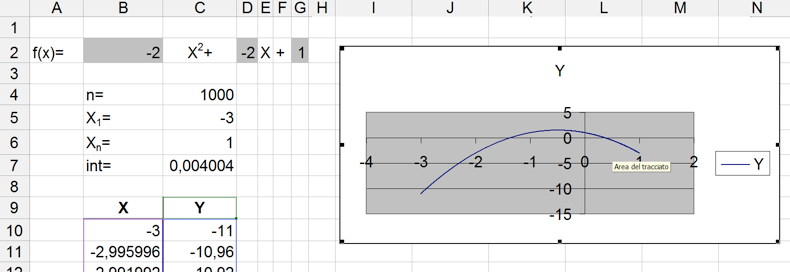
Otterremo quindi un grafico dinamico simile a questo:
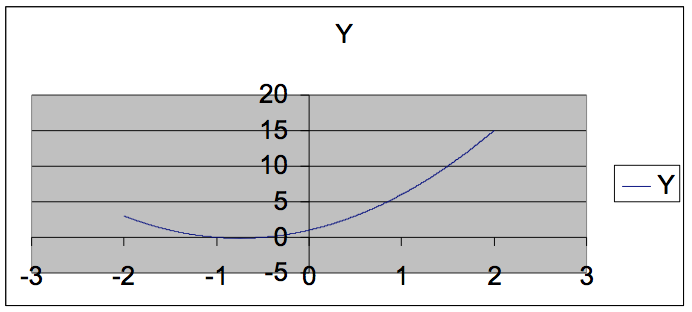
Dinamico perché sarà sufficiente variare l'intervallo X1 -Xn e/o i coefficienti che definiscono la funzione, per ottenere istantaneamente e senza interventi ulteriori, un nuovo grafico: