Algebra dell'orologio
- Classi
terze
- Durata
2 ore
- Scopo
Realizzare una tabella "dinamica" di operazioni modulari.
- Prerequisiti
Uso della funzione SE e della formattazione condizionata nel foglio elettronico.
Introduzione
L'aritmetica modulare, detta anche "algebra dell'orologio" perche' le ore rappresentano uno degli esempi classici di operazione in "modulo", si basa sull'aritmetica degli interi e, in sostanza, sulle operazioni in modulo n.
Prendiamo un numero M ed applichiamo il modulo n: il risultato di M modulo n sara' il resto della divisione intera:
5 modulo 2 = 1
perche' 5/2= 2 con resto 1
oppure, come spesso si fa per le ore
13 modulo 12 = 1
infatti, le ore 13 sono spesso indicate come l'ora 1 del pomeriggio.
Per maggiori approfondimenti teorici sull'algebra dell'orologio si rimanda allo specifico modulo teorico.
Dalla teoria alla pratica
In questo caso, creeremo due tabelle, una per la somma ed una per la moltiplicazione ed inseriremo, all'incrocio di ogni riga con ogni colonna il risultato dei due operatori con il modulo del numero riportato in alto a sinistra come si può vedere in figura
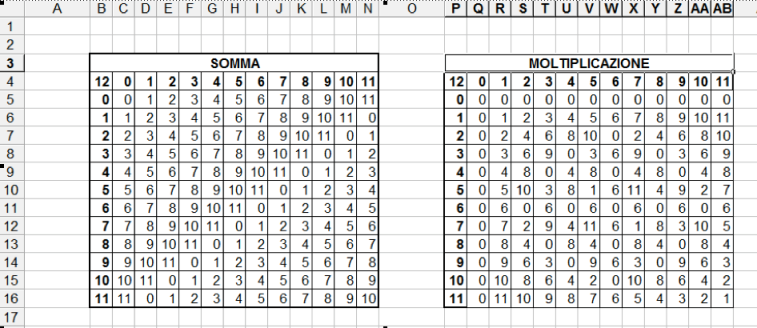
La costruzione sembra semplice ma, per evitare perdite di tempo per tabelle che possono avere anche piu' righe e colonne, la formula all'interno dell'incrocio deve essere costruita con un misto di indirizzamenti assoluti (con l'uso del simbolo $ per bloccare la riga e/o la colonna) e relativi (senza $) in modo che la formula "campione" sia poi "trascinata" automaticamente in ogni cella senza modifiche ulteriori. La formula fara' riferimento alla funzione resto ed alla operazione prevista: la cella c5 conterra' la funzione RESTO(dividendo;divisore) della somma di C4 e B5 modulo B4; in questo modo sarà possibile modificare il valore del modulo a piacere semplicemente cambiando il valore nella cella B4 per la somma o P4 per la moltiplicazione.
L'occasione potrebbe essere utile per introdurre (solo per Excel) la notazione in RC (riga e colonna); in questa modalita', attivabile sono in Excel da menu' Strumenti -> Opzioni -> Generale e poi spunta su Stile di riferimento R1C1, i riferimenti alle celle non sono in lettere e numeri ma solo in numeri anche per le colonne; per esempio la cella B4 diventa per R4C2 (cioè riga 4 colonna 2) e la cella C15 diventa R15C3. Ma, mentre per l'indirizzamento assoluto è solo un cambio di notazione, la vera novità rispetto alla rappresentazione tradizionale e' legata agli indirizzamenti relativi; se si volesse fare riferimento alla cella immediatamente a sinistra della cella R2C2 la scrittura sarebbe R2C[-1] cioè la colonna corrente (quella in cui sto scrivendo) -1 (cioe' quella subito a sinistra della corrente); analogamente se dovessi fare riferimento ad una cella 3 righe più in basso e 2 colonne più a destra, scriverei R[+3]C[+2]. Provi lo studente a verificare se, con lo stile di riferimento R1C1, la formula base che dovra' essere copiata in tutta la tabella risulta più semplice da costruire.
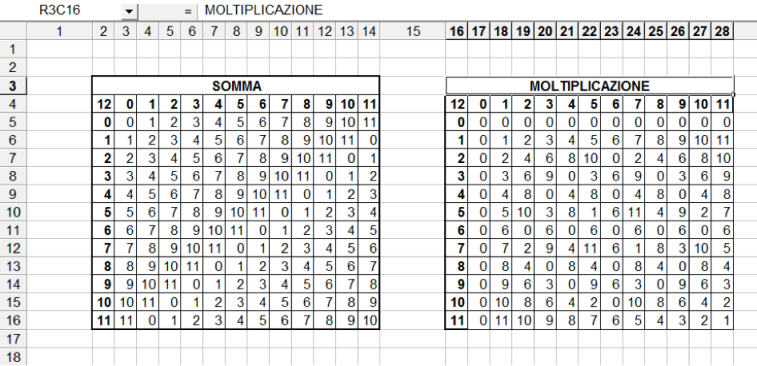
Si noti, nella figura, lo stile di riferimento della cella corrente in alto a sinistra.
Per migliorare la leggibilita' della tabella, sarebbe utile che siano omesse le celle "ridondanti" cioè tutte quelle celle che fanno riferimento a righe e colonne superiori o uguali al modulo dato che, in questo caso, sono una riproposizione degli stessi valori.
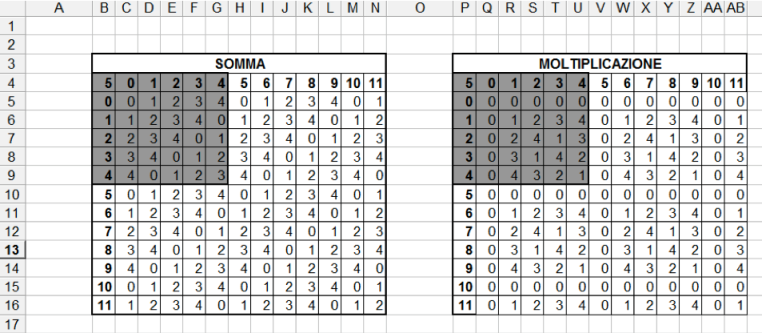
Si noti in figura che i valori oltre il quadrato grigio sono riproposizioni degli stessi valori i sequenza presenti all'interno dello stesso.
La modifica proposta non e' legata all'algebra modulare ma permette di affinare alcune tecniche utili in altre applicazioni esplorando le possibilita' offerte dal foglio elettronico oltre a consentire di rendere dinamica la rappresentazione della tabella.
La tecnica da usare è quella dell'illusione ottica; i valori all'interno delle tabelle possono "sparire" in virtu' di un semplice SE: se la riga e la colonna esterne alla tabella sono inferiori al numero indicato in alto a sinistra allora si scrivera' la formula, altrimenti si scriverà una cella vuota (""); nello scrivere la funzione SE si porra' la massima attenzione ai riferimenti assoluti e relativi in modo che la formula "base" possa essere copiata senza variazioni in tutte le altre celle.
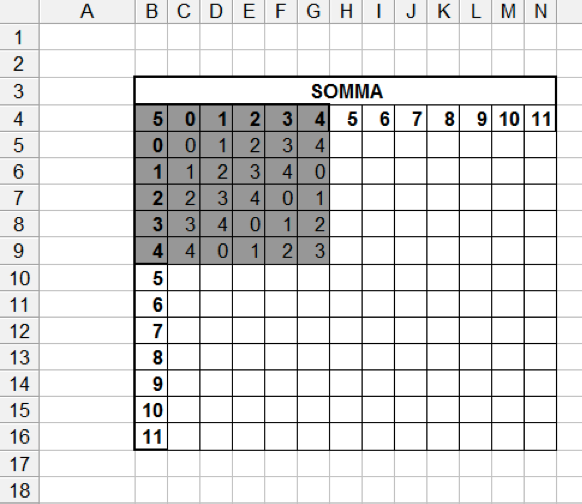
La dimensione della tabella variera' in funzione del numero indicato in alto a sinistra. Come si può notare però, gli indicatori di riga e colonna all'estremita' della tabella sono ancora visibili; per renderli "invisibili" non è però possibile utilizzare la funzione se perche' i valori stessi sono riferimento per le celle interne e devono essere presenti. Per farli "sparire" è opportuno usare la formattazione condizionata che, nel caso il valore sia superiore od uguale al modulo, ne modifichi l'aspetto con bianco su bianco in modo da renderlo "invisibile".
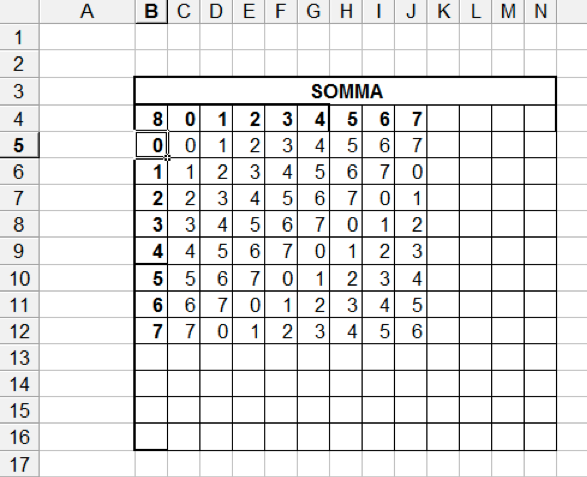
esempio di tabella in modulo 8