Equazioni di secondo grado
- Classi
terze
- Durata
4 ore
- Scopo
Realizzare un'applicazione con il foglio elettronico che fornisca le soluzioni ad un'equazione di 2° grado.
- Prerequisiti
Uso della funzione SE nel foglio elettronico.
Introduzione
Come sempre lo scopo della nostra attività non è quello di trovare la soluzione ad una specifica equazione di secondo grado, ma impostare un metodo che consenta di risolvere qualsiasi equazione di secondo grado "gestendo" anche situazioni particolari e consentendo un facile inserimento dell'equazione stessa. Un'equazione di secondo grado si presenta nella forma generale ax2 + bx + c = 0 dove a, b e c sono chiamati coefficienti e sono rappresentati da numero reali a caratterizzare la specifica equazione; le due soluzioni, generalmente indicate come X1 e X2, sono ottenibili da una formula piuttosto conosciuta
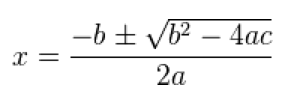
- due soluzioni distinte
- due soluzioni coincidenti
- nessuna soluzione in campo reale
Dalla teoria alla pratica
Utilizzando il foglio elettronico per questo esercizio, un aspetto da non trascurare è la scrittura dell'equazione; l'equazione deve essere descritta attraverso i coefficienti a,b e c ma la loro presentazione può rendere semplice o complicata l'interpretazione dell'equazione stessa da parte dell'utilizzatore che, rammentiamolo, spesso non è colui che ha scritto il foglio elettronico.
Una soluzione semplice per inserire e proporre l'equazione può essere quella indicata di seguito
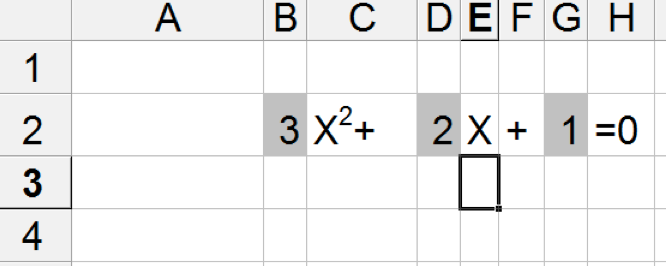
Come si può notare le celle con sfondo grigio sono quelle dove vanno inseriti i coefficienti che permettono di descrivere una qualsiasi equazione (quello riportato in figura è solo un esempio); nel contempo l'equazione è perfettamente riconoscibile come tale. Ora non resterà che individuare delle celle nelle quali proporre le soluzioni a partire dalla formula risolutiva prima descritta. Non si deve dimenticare però che, nel caso di delta negativo o nullo, si presentano delle situazioni che vanno ben evidenziate; quindi, anche per semplificare le operazioni di controllo, vale la pena di calcolare il delta in una cella intermedia.

Le formule non presentano particolari insidie ma si deve fare attenzione alla priorità degli operatori aritmetici ed all'uso delle parentesi.
Come detto in precedenza ci sono delle situazioni in cui non c'è soluzione nel campo reale ed il foglio elettronico reagisce con degli errori:
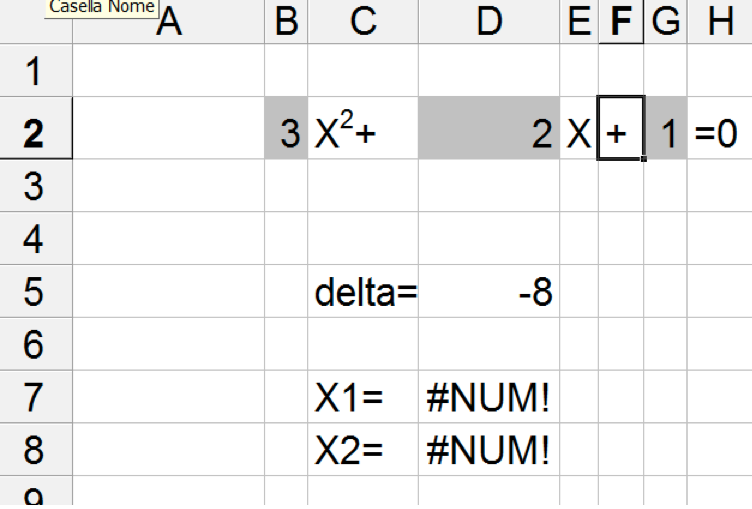
oppure nel caso in cui il coefficiente a valga zero non abbiamo più un'equazione di secondo grado:

Come gestire queste "anomalie" ? utilizzando la funzione SE anche nella sua forma "annidata" o "nidificata" ma così è un SE annidato ? in sostanza è una funzione SE dentro un'altra funzione SE e serve per gestire non 2 ma 3 o più possibilità a fronte di 2 o più condizioni:
SE "normale"
SE (condizione; azione per vero; azione per falso)
SE "annidato"
SE(condizione1 ; azione per vero 1; SE(condizione2 ; azione per vero 2 ; azione per falso))
Come si può notare nel primo caso le possibili azioni sono 2 (azione per vero, azione per falso) mentre nel secondo caso sono 3 (azione per vero 1, azione per vero 2, azione per falso).
Ma come si applica il SE annidato al contesto ?
Nel caso volessimo gestire solo la presenza o l"assenza di soluzioni, sarebbe sufficiente un solo SE:
SE(delta < 0; "IMPOSSIBILE" ; esegui la formula risolutiva)
ottenendo un risultato simile a questo
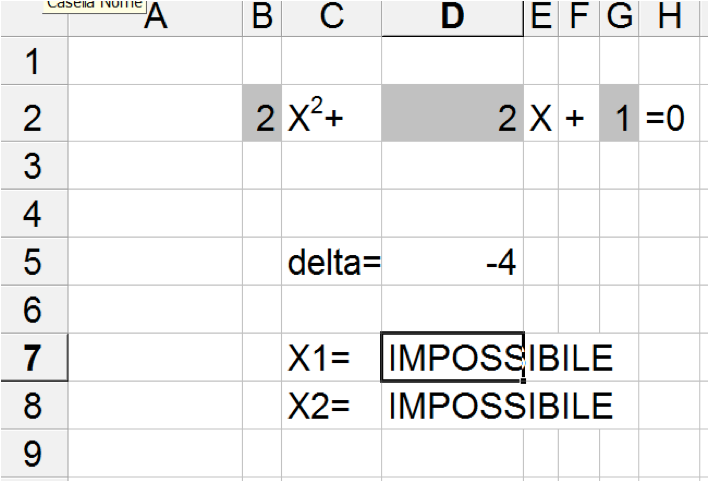
Ma se, nel caso avessimo un delta pari a zero, volessimo mettere in rilevo questa situazione eccezionale scrivendo "uguale a X" nella casella della soluzione X2, allora la casella che contiene la soluzione X2 avrebbe 3 possibili esiti:
SE(delta<0;"IMPOSSIBILE"SE(delta = 0; "UGUALE A X1"; =soluzione per X2))
presentando una situazione come quella nella figura seguente

La stessa tecnica può essere usata per indicare che l?equazione non è di secondo grado se il coefficiente a è pari a zero.
Un'ultima annotazione riguarda la presentazione dei risultati: generalmente le soluzioni fratte vengono proposte nella loro forma frazionaria (1/2) mentre il foglio elettronico le propone come risultato nella frazione (0,5) .
Questa difformità può essere corretta utilizzando una formattazione personalizzata delle celle con le soluzioni.