Sistemi di numerazione
- Classi
terze
- Durata
6 ore
- Scopo
Capire i sistemi di numerazione a base non decimale; attuare procedure automatiche per realizzare conversioni da base qualsiasi a base decimale e viceversa.
- Prerequisiti
Uso della funzione SE e della formattazione condizionata nel foglio elettronico.
Introduzione
Generalmente quando si fa riferimento ai sistemi di numerazione si pensa al sistema decimale; in realtà il più usato è sicuramente il sistema binario, se non altro perché utilizzato in tutti i sistemi digitali (computer, ma non solo) per elaborare, archiviare e trasmettere dati. La scelta di usare un sistema basato su due sole cifre, 0 e 1 (corrispondenti generalmente anche ad uno stato di spento/acceso oppure falso/vero) ha una ragione piuttosto evidente nella semplicità di trattare il segnale elettrico binario all'interno dei sistemi elettronici complessi come i computer; appare evidente che progettare e realizzare dei circuiti elettronici per riconoscere la presenza o l'assenza di un segnale elettrico è molto più semplice che riconoscere una gradualità di valori in scala (per esempio da 0 a 5 o da 0 a 10); fra l'altro sistemi elettronici basati su un sistema decimale sarebbero estremamente complessi e lenti e genererebbero errori ben più frequenti. Fin dai loro albori, gli elaboratori elettronici si sono basato sui principi dell'algebra booleana (George Boole) e sul sistema binario
Il sistema decimale è un sistema posizionale nel quale ogni cifra ha un "peso" che dipende dalla posizione che assume partendo da destra (cifre meno significative) e andando verso sinistra (cifre più significative). Più in generale quindi possiamo rappresentare un numero decimale come la somma dei fattori che lo compongono come più volte è stato fatto alla scuola primaria (per evitare di confondere il numero decimale 111 con il numero binario 111, quando si opera con sistemi numerici diversi è consuetudine indicare il numero fra parentesi e con al base come pedice; per esempio (111)10 oppure (111)2 ):
(2003)10 = 3u + 0da + 0h + 2k
siccome:
u = unità = 1 = 100
da= decine = 10 = 101
h = centinaia = 100 = 102
k = migliaia = 1000 = 103
allora possiamo scrivere anche
(2003)10 = 3 x 100 + 0 x 101 + 0 x 102 + 2 x 103
Per una definizione più formale di sistema di numerazione posizionale possiamo fare riferimento a quanto segue:
- si sceglie un qualsiasi numero naturale b (diverso da zero e da uno), che chiameremo base
- si scelgono c simboli diversi, che chiameremo cifre
- si compongono i numeri tenendo presente che il valore di ogni cifra va moltiplicato per:
- b0 cioè 1 (unità) se è l'ultima cifra alla destra del numero che stiamo considerando
- b1 cioè b se è la seconda cifra da destra,
- b2 se è la terza cifra da destra,
- e così via, bn-1 se è la n-esima cifra da destra
- la somma di tutti i valori così ottenuti è il numero che stiamo considerando; se consideriamo la cifra meno significativa (quella più a destra) come C0 e quella più a sinistra come cifra più significativa Cn possiamo scrivere
(CnCn-1Cn-2 ... C2C1C0)b = C0 x b0 + C1 x b1 + C2 x b2 + .... + Cn-2 x bn-2 + C n-1x bn-1 + Cn-2 x bn-2
e quindi per esempio:
(2123)10 = 3 x 100+ 2 x 101+ 1 x 102 + 2 x 103 = 3x1 + 2x10 + 1x100 + 2x1000 = (2123)10
Come effettuare la conversione da una base qualsiasi a base decimale
Analogamente al sistema decimale posizionale, anche il sistema binario è un sistema posizionale in cui la base è rappresentata dal numero 2 e le cifre dai soli valori 0 e 1, la somma dei singoli valori scomposti è però espressa in base decimale
(CnCn-1Cn-2.... C2C1C0) = C0 x 20 + C1 x 21 + C2 x 22 + ... + Cn-2 x 2n-2 + C n-1 x 2n-1 + Cn x 2n
(110)2= 0 x 20 + 1 x 21 + 1 x 22 = 0 x 1 + 1 x 2 + 1 x 4 = (5)10
Quindi, per effettuare la conversione da base binaria a base decimale, è necessario procedere come per una scomposizione sommando poi i singoli fattori. Da notare che, come vedremo più avanti, lo stesso procedimento si può usare per qualsiasi sistema posizionale. Un'altra interessante particolarità del sistema binario è che si può capire se il numero decimale convertito sarà pari o dispari solo osservando l'ultima cifra del numero binario (se è 0 sarà pari, se è 1 sarà dispari).
Dalla teoria alla pratica
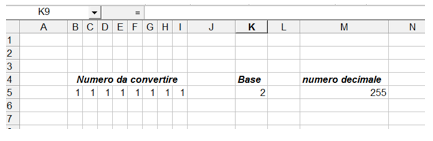
Traducendo la teoria in pratica si può procedere individuando nel foglio elettronico un'area (un insieme di celle, tipicamente 8 per il sistema binario) nella quale inserire il valore da convertire distinto per singola cifra, una cella nella quale indicare la base, ed una cella nella quale verrà fornito il numero convertito. Il numero decimale convertito sarà facilmente ottenibile utilizzando le formule descritte in precedenza (nell'esempio in figura M5= I5*K50 + H5*K51 + ....) in questo modo sarà possibile convertire anche numeri con basi diverse da 2 (es. 8).
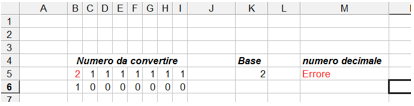
Come avviene spesso, il sistema deve tener conto anche della presenza di valori in ingresso coerenti; se scrivessi una cifra superiore od uguale alla base, per esempio 3, questo dato sarebbe incompatibile con il sistema binario ed il software dovrebbe indicare tale anomalia.
Questa situazione può essere gestita nel seguente modo:
- la cifra in rosso con una formattazione condizionata
- il flag di controllo (celle della riga 6 che assumono solo i valori 0 e 1) con una clausola SE riferita alla cella soprastante.
- la scritta Errore controllando la somma dei bit di controllo e se questa è maggiore di 0, scrivere Errore altrimenti con il risultato della formula già individuata
I flag di controllo possono essere colorati di bianco su sfondo bianco in modo da non essere visibili.
Il sistema Esadecimale
Il sistema numerico esadecimale (spesso abbreviato come esa o hex) è un sistema numerico posizionale in base 16, cioè che utilizza 16 simboli invece dei 10 del sistema numerico decimale tradizionale. Per l'esadecimale si usano in genere simboli da 0 a 9 per le prime dieci cifre, e poi le lettere da A a F per le successive sei cifre, per un totale di 16 simboli. E' usato in informatica nel linguaggio Assembler per la sua caratteristica di raggruppare insiemi di 4 cifre binarie chiamati anche semibyte o nibble
(F)16 = (1 1 1 1 )2
(C)16 = (1 1 0 0 )2
(4)16 = (1 0 0 0)2
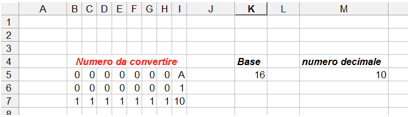
La nostra applicazione potrebbe, con alcune modifiche, convertire anche numeri esadecimali ma per farlo è necessario gestire cifre non numeriche la letterali; in pratica è necessario convertire la lettera A nel corrispondente valore 10, lettera B nel corrispondente valore 11 e così via.
Per procedere è necessario gestire un'ulteriore valore che diverrà poi il valore della cifra da moltiplicare per la base elevata alla posizione (nell'esempio in figura M5= I7*K5^0 + H7*K5^1 + G7*K5^1 + .....)
La trasformazione da cifra esadecimale letterale al suo valore effettivo può essere effettuata utilizzando la funzione Excel CODICE che restituisce il corrispondente valore ASCII (un sistema che fa corrispondere ad ogni lettera o simbolo un numero fra 0 e 225 secondo una tabella chiamata appunto ASCII - American Standard Code for Information Interchange - ovvero Codice Standard Americano[1] per lo Scambio di Informazioni) della lettera indicata (es. CODICE(I5) = 65, CODICE("B")= 66, ecc.).
Come è possibile intuire la cella I7 conterrà la formula = CODICE(I5) - 55; infatti sottraendo 55 al numero ASCII ottenuto si ottiene proprio il valore della cifra esadecimale (nel caso in esame la "A" vale 10); naturalmente la conversione deve avvenire solo se la cifra non è già un numero nel qual caso va riportato così com'è. Questa ulteriore evoluzione del procedimento permette al nostro sistema di convertire un numero da base qualsiasi, inferiore od uguale all'esadecimale, nel corrispondente valore decimale. Modificando alcune funzioni ma adottando il medesimo principio è possibile usare questo procedimento anche con JavaScript per chi possedesse delle nozioni di base di programmazione.
Come effettuare la conversione da una base decimale a base qualsiasi
Naturalmente per completare il nostro procedimento è necessario effettuare anche la conversione opposta passando da un numero decimale al corrispondente valore in una base fra quelle già viste.
Come procedere
Ricordiamo che un numero è composto di cifre il cui peso dipende dalla posizione
Cn Cn-1 ... C3 C2 C1 C0
se il numero in base 10 da convertire è N e la base nella quale convertirlo è b, si potrà procedere nel seguente modo:
Per determinare il valore delle cifre nella nuova base scelta si deve calcolare la divisione intera di N per b: N/b=N' con resto R' R' è la cifra più a destra nella rappresentazione in base b di N, cioè C0 = R' Si divide N'/b ottenendo N'/b = N'' con resto R'' e si ha che C1 = R'' Si ripete il procedimento fino a quando il risultato della divisione N? è uguale a 0
Complicato ? consideriamo ad esempio il numero (345)10 e calcoliamo la sua rappresentazione in base sedici:
345/16= 21 resto 9
21/16 = 1 resto 5
1/16 = 0 resto 1
Leggendo i resti dal basso verso l'alto, si ha che la rappresentazione esadecimale del numero decimale (345)10 è (159)16
Come possiamo tradurre questa operazione nel foglio elettronico?
Nell'esempio sottostante proviamo a convertire il numero 52 nel corrispondente valore binario (infatti nella casella D4 che rappresenta la base il valore è 2).
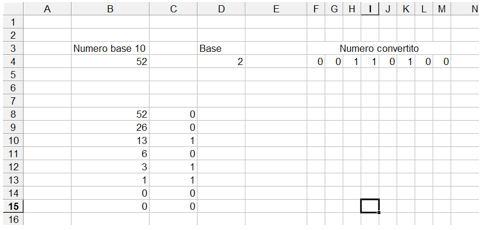
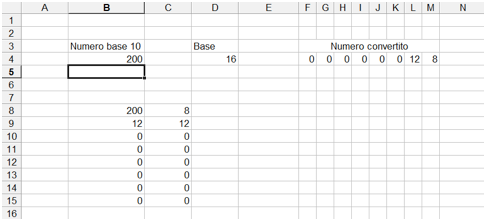
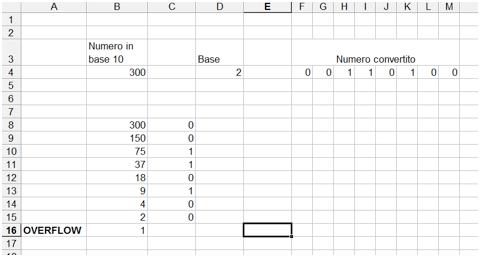
Nelle celle da B8 a C15 viene effettuata proprio l'operazione descritta sopra utilizzando due funzioni di Excel; la prima si chiama RESTO è restituisce il resto della divisione intera fra due numeri, la seconda si chiama INT e permette di ottenere il risultato intero della stessa divisione. I risultati della colonna C vengono inseriti nelle celle del numero convertito a rappresentare le cifre così ottenute. Da notare almeno 3 cose: la prima è che possibile, modificando solo la base, convertire il numero decimale in qualsiasi base ma con l'accortezza di gestire le cifre esadecimali; infatti il risultato della divisione intera va da 0 a base-1 e quindi è possibile ottenere, come nell'esempio, il valore 12 che va convertito nella lettera "C" utilizzando la funzione CODICE.CARATT(65) che restituisce "A" oppure CODICE.CARATT(55+L4) che restituisce la lettera "C" analogamente a quanto fatto nella conversione da esadecimale a decimale con i codici ASCII. La seconda è che si deve tener conto del possibile overflow, cioè della possibilità che il numero da convertire sia troppo grande per le cifre predisposte e quindi il risultato dell'ultima divisione intera non sia 0; sarà opportuno prevedere un apposito controllo per segnalare errori di overflow.
Il terzo aspetto interessante è che questa procedura è autovalidante: in pratica è possibile verificarne la correttezza usando la stessa procedura: per esempio (255)10 diventa, usando la procedura di conversione da decimale a binaria, (11111111)2; inserendo poi il risultato per la conversione opposta, se le procedure sono costruite correttamente, otterremo (255)10 altrimenti avremo un malfunzionamento.