Teoremi
Analizzeremo alcuni lemmi ovvero dei teoremi che serviranno ad introdurci alle dimostrazioni del teorema dei seni ed il teorema del coseno.
Teorema dell'angolo al centro
Teorema: L'angolo al centro della circonferenza è il doppio di un qualsiasi angolo alla circonferenza che insiste sullo stesso arco.
Dimostrazione
Dividiamo la dimostrazione del teorema in tre casi.
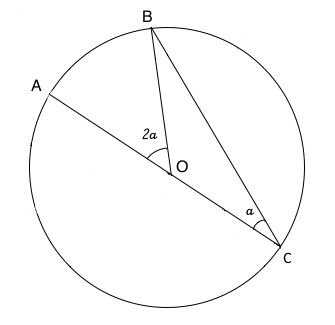
Il primo caso è caratterizzato dal fatto che il lato dell'angolo alla circonferenza CA passa per il centro della circonferenza O. Va dimostrato che l'angolo alla circonferenza ACB che in figura è indicato con α è la metà dell'angolo al cento AOB, entrambi gli angoli insistono infatti sullo stesso arco AB. Si consideri il triangolo BOC. Si tratta di un triangolo isoscele in quanto due lati BO e OC corrispondono al raggio della circonferenza. Gli angoli opposti ai due lati uguali sono pure essi uguali. In figura sono indicati con α. L'angolo BOC è 180o-2α in quanto la somma degli angoli interni di un qualsiasi triangolo è 180o. L'angolo BOC sommato all'angolo AOB deve dare 180o, l'angolo AOB dev'essere quindi 2α che è quello che si voleva dimostrare.
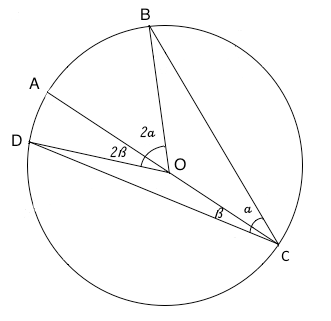
Il secondo caso prevede che il centro della circonferenza O è contenuto nell'angolo alla circonferenza DCB. In figura è disegnato il diametro COA per meglio notare che l'angolo AOB è il doppio dell'angolo ACB infatti siamo ricaduti nel caso 1, analogamente l'angolo AOD è il doppio dell'angolo ACD. L'angolo DOB può essere espresso come somma degli angoli DOA e AOB ovvero DOB=2α+2β=2(α+β) e analogamente l'angolo BCD può essere espresso come somma degli angoli BCA e ACD ovvero BCD=α+β. Dalle due relazioni: DOB=2(α+β) e BCD= α+β, si può quindi concludere che l'angolo DOB è il doppio dell'angolo BCD.
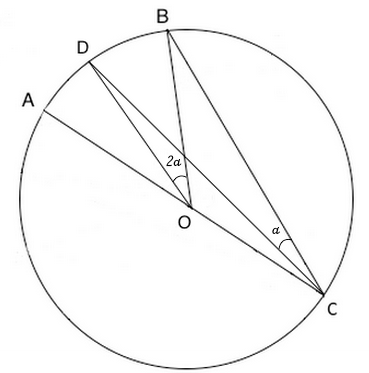
Nel terzo caso il centro della circonferenza O è esterno all'angolo alla circonferenza DCB. In figura è disegnato il diametro COA per meglio notare che l'angolo AOB è il doppio dell'angolo ACB infatti siamo ricaduti nel caso 1, analogamente l'angolo AOD è il doppio dell'angolo ACD. L'angolo DOB può essere espresso come differenza degli angoli AOB E AOD ovvero DOB=2α-2β=2(α-β) e analogamente l'angolo BCD può essere espresso come differenza degli angoli ACB e ACD ovvero BCD=α-β. Dalle due relazioni: DOB=2(α-β) e BCD= α+β, si può quindi concludere che l'angolo DOB è il doppio dell'angolo BCD.
In questo modo, suddividendo la dimostrazione nei tre casi visti, si sono considerati tutti i casi possibili.
Teorema del triangolo inscritto in una semicirconferenza
Teorema: Un triangolo inscritto in una semicirconferenza è rettangolo.
Dimostrazione
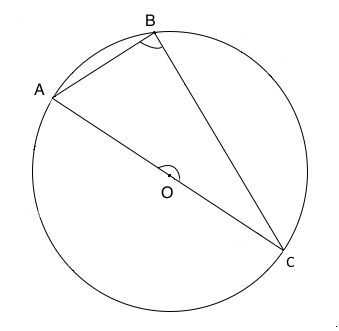
Nella figura è rappresentato un triangolo inscritto in una semicirconferenza ovvero l'ipotenusa del triangolo corrisponde al diametro della circonferenza. L'angolo in B è un angolo alla circonferenza che insiste su di un arco uguale alla semicirconferenza. L'angolo in O è invece un angolo al centro della circonferenza che insiste sullo stesso arco. L'angolo in O è un angolo piatto quindi per il teorema precedente, ovvero per il teorema dell'angolo al centro, l'angolo in B è la sua metà ovvero un angolo retto.
Teorema del quadrilatero inscritto in una circonferenza
Teorema: Un quadrilatero inscritto in una circonferenza ha gli angoli opposti supplementari.
Dimostrazione
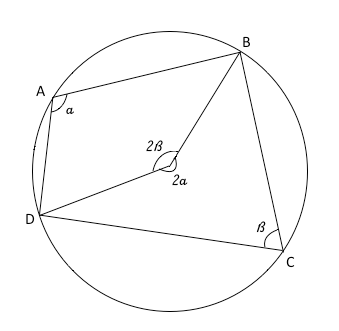
Nella figura è rappresentato un quadrilatero ABCD inscritto in una circonferenza. L'angolo β che ha il vertice in C, per il teorema visto in precedenza, è la metà dell'angolo al centro della circonferenza che insiste sull'arco DAB, che in figura è l'arco piu' piccolo. Analogamente l'angolo α che ha vertice in A è la metà dell'angolo al centro della circonferenza che insiste sull'arco DCB ovvero, in figura, quello che è l'arco più grande. La somma di 2α+2β costituisce un angolo giro, per cui α+β è la meta' ovvero un angolo piatto, quindi α e β sono due angoli supplementari, ma α e β sono proprio i due angoli opposti del quadrilatero inscritto.
Teorema della corda
Teorema: In una circonferenza, la misura di una corda, è data dal prodotto del diametro moltiplicato per il seno per l'angolo alla circonferenza (indifferentemente uno dei due angoli alla circonferenza) che insiste sulla corda.
Dimostrazione
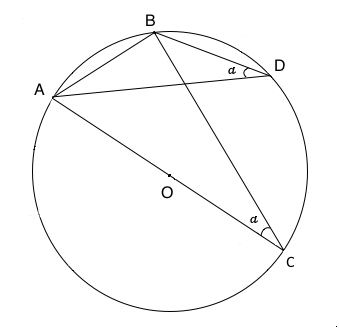
Nella figura è rappresentato un angolo alla circonferenza che insiste sull'arco AB, quello minore. L'angolo che ha vertice in D è uguale all'angolo alla circonferenza che ha un lato corrispondente al diametro in figura l'angolo in C. Questi due angoli sono uguali tra loro in quanto entrambi insistono sull'arco AB e quindi entrambi sono la metà dell'angolo al centro che insiste sullo stesso arco. In figura vengono infatti indicati entrambi con α. Il triangolo ABC avendo l'ipotenusa corrispondente al diametro è un triangolo rettangolo, possiamo scrivere quindi le relazioni individuate per i triangoli rettangoli ovvero:
AB=AC sinα
ovvero:
AB=2r sinα
dove si è indicato con r il raggio della circonferenza, che è cio che si vuol dimostrare. Nella figura di sotto si è considerato l'angolo alla circonferenza che insiste sull'arco AB maggiore. In tal caso l'angolo ADB è 180o-α e questo lo si ottiene applicando, al quadrilatero ADBC, il teorema del quadrilatero inscritto in una circonferenza.
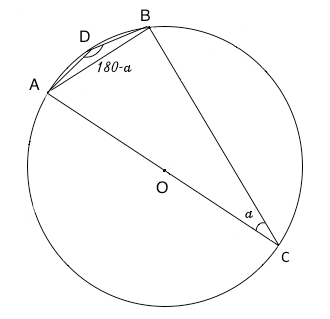
Dalla relazione sin180o-α=sinα si può quindi affermare che il teorema della corda rimane valido anche in tal caso.
Teorema dei seni, detto anche teorema di Eulero
Teorema: In un triangolo è costante il rapporto tra la misura di ciascun lato e il seno dell'angolo opposto.
Dimostrazione
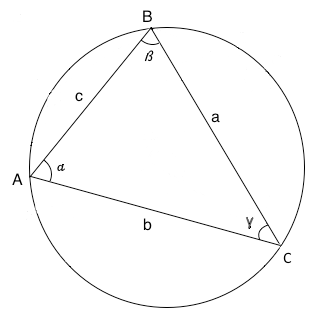
Si noti che un triangolo è sempre inscrittibile in una circonferenza. In figura al triangolo ABC possiamo applicare il teorema della corda da cui:
a=2rsinα b=2rsinβ c=2rsinγ
dove r è il raggio della circonferenza che inscrive il triangolo. Da tali relazioni ne consegue che:
2r=a/sinα 2r=b/sinβ 2r=c/sinγ
e per la proprietà transitiva dell'uguaglianza:
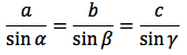
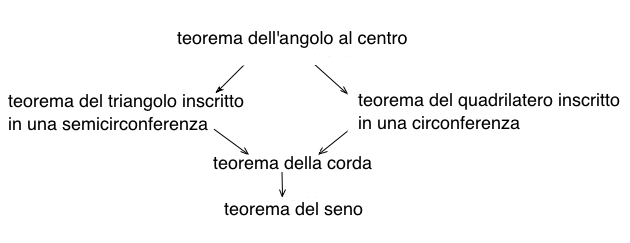
Per memorizzare meglio la sucessione dei teoremi che portano alla dimostrazione del teorema dei seni, si noti che dal teorema dell'angolo al centro ne conseguono i teoremi del triangolo inscritto in una semicirconferenza e del quadrilatero inscritto in una circonferenza. Da questi due teoremi ne consegue il teorema della corda dal quale poi a sua volta ne deriva il teorema dei seni. Questi cinque teoremi sono dunque legati al seguente schema.
Teorema delle proiezioni
Teorema: In un triangolo un lato è dato dalla somma degli altri due lati moltiplicati ciascuno per il coseno dell'angolo adiacente al lato stesso.
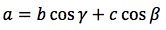
Dimostrazione
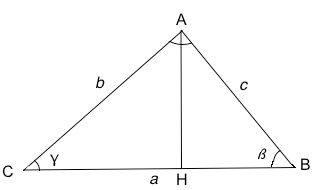
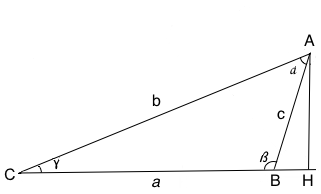
In figura H sia il piede dell'altezza relativa al lato a, i due triangoli ABH ed ACH sono rettangoli in quanto l'angolo in H è retto, si può quindi scrivere che BC=BH+HC, applichiamo quindi le relazioni relative ai triangoli rettangoli per cui: CH=b cosγ, HB=c cosβ per cui: a=b cosγ+c cosβ La relazione rimane valida anche nel caso in cui β sia un angolo ottuso, anche in questo caso H sia il piede dell'altezza relativa al lato a, i due triangoli ABH ed ACH sono rettangoli in quanto l'angolo in H è retto, quindi: CB=CH-BH, ma CH=b cos γ e BH=c cos(180o-β) quindi: a=b cosγ-c cos(180o-β) ma cos(180o-β)=-cosβ, per cui a=b cosγ-(-c cos(β) ovvero: a=b cosγ+c cosβ
Teorema del coseno, detto anche teorema di Carnot
Teorema: in un triangolo un lato al quadrato è dato dalla somma degli altri due lati al quadrato da cui si deve togliere il prodotto degli altri due lati moltiplicati per il coseno dell'angolo che sta opposto al lato stesso.
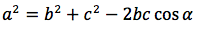
Dimostrazione
Per il teorema delle proiezioni si può scrivere:
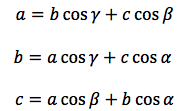
moltiplicando per a la prima relazione, per -b la seconda e per -c la terza si ottiene:
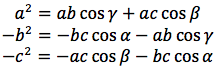
sommando membro a membro i termini delle tre relazini e semplificando:
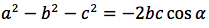
ricaviamo a:
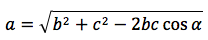
Se l'angolo compreso è retto il coseno dell'angolo retto è zero per cui il teorema del coseno si trasforma nel teorema di Pitagora, per questo motivo il teorema del coseno oltre che teorema di Carnot, viene anche chiamato teorema di Pitagora generalizzato.
Con opportuni semplici accorgimenti si ricavano analoghe formule oltre che per il lato a pure per i lati b, c:
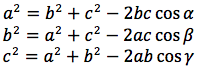
Si può ricavare anche il cosα in funzione dei lati:
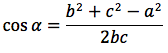
e con la funzione inversa, arcocoseno, si determina l'angolo α in funzione dei tre lati:
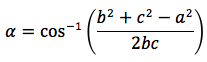
Si noti che dal teorema delle proiezioni ne consegue il teorema del coseno, questi due teoremi sono dunque legati al seguente schema.