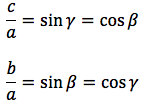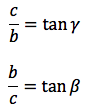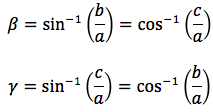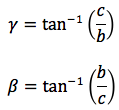Relazioni trigonometriche
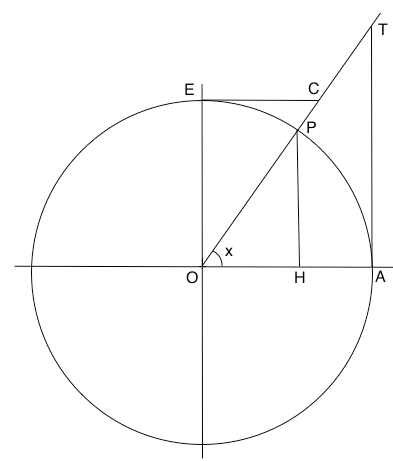
In figura è rappresentata la circonferenza goniometrica. Il raggio della circonferenza goniometrica vale 1. Sia P un punto vincolato a percorrere la circonferenza in senso antiorario. Le coordinate del punto P sono rispettivamente cosx e sinx. L'ordinata del punto T è la tanx e l'ascissa del punto C è la cotx. Per semplificare le notazioni, l'angolo "variabile" POH è stato indicato come angolo x come già è stato spiegato in funzioni goniometriche.
Per definizione si ha quindi che:
OP=1
PH=sinx
OH=cosx
AT=tanx
EC=cotx
Relazioni fondamentali
Considerato che il triangolo OPH è rettangolo, per il teorema di Pitagora si avrà HP2+OH2=1 ovvero sostituendo si ricava quella che viene chiamata la prima relazione fondamentale della trigonometria:
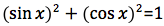
Si considerino i due triangoli OTK e OPH, essi sono simili poiché sono entrambi triangoli rettangoli ed hanno un angolo in comune. Dalla similitudine ne consegue la seguente proporzione: PH:OH= TK:OK ovvero sinx:cosx=tanx:1 da ciò si ricava quella che viene chiamata la seconda relazione fondamentale della trigonometria:
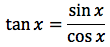
Si considerino i due triangoli OTA e OPH, essi sono simili poiché sono entrambi triangoli rettangoli ed hanno l'angolo POH uguale a EOC. I due triangoli sono simili da cui ne consegue la seguente proporzione: EC:OE=OH:PH ovvero =cotx:1=cosx:sinx da ciò si ricava: cotx=cosx/sinx, ovvero la cotangente è la funzione reciproca della tangente.
Relazioni in un triangolo rettangolo
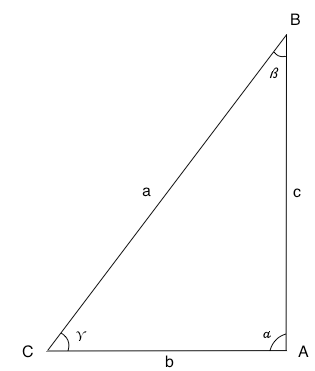
A destra in figura, supponiamo di avere un triangolo rettangolo con angolo retto in A e con l'angolo γ uguale all'angolo x della circonferenza goniometrica. I due triangoli ABC e POH sono simili, poiché hanno due angoli uguali.
I lati dei due triangoli sono quindi proporzionali e si possono scrivere le seguenti proporzioni:
OP:PH=CB:AB ovvero, tenendo presente che il raggio della circonferenza trigonometrica è 1 1:sinx=a:c da cui sinx=c/a da cui c=a*sinx, generalizzando, un cateto è dato dal prodotto dell'ipotenusa moltiplicata per il seno dell'angolo opposto.
OP:OH=a:b ovvero 1:cosx=a:b da cui cosx=b/a da cui b=a*cosx, generalizzando, un cateto è dato dal prodotto dell'ipotenusa moltiplicata per il coseno dell'angolo adiacente.
PH:OH=AB:AC ovvero sinx:cosx=c:b da cui sinx/cosx=c/b ovvero dato che tanx=sinx/cosx, tanx=c/b da cui c=btanx, generalizzando, un cateto è dato dal prodotto dell'altro cateto moltiplicato per la tangente dell'angolo opposto.
Si sono individuate quindi, le seguenti relazioni: