Funzioni esponenziali
La funzione esponenziale f(x)=bx pensata come funzione f: R → R è una funzione iniettiva ma non suriettiva, lo si nota dai relativi grafici poichè le orizzontali del tipo y=p con p numero positivo hanno un'intersezione con il grafico della funzione invece le orizzontali del tipo y=n con n negativo non hanno intersezione come non ha intersezioni l'asse x stessa. Per rendere la funzione biettiva e quindi invertibile si dovrà restringere il codominio all'insieme immagine ovvero R+. Si studiano due casi di funzioni esponenziali a seconda che la base assuma un valore compreso tra zero e uno oppure un valore maggiore di uno. Non ha interesse il caso in cui la base b sia uguale a zero poichè y=0x corrisponde all'asse delle x e non ha interesse il caso in cui la base b sia uguale a uno poichè y=1x corrisponde alla retta orizzontale y=1. Non si studia, e non avrebbe senso farlo, studiare la funzione esponenziale con la base negativa.
L'esponente reale
L'introduzione dei numeri relativi è dovuta al fatto che nell'insieme dei numeri naturali manca l'opposto. L'introduzione dei numeri razionali è dovuta al fatto che nell'insieme dei numeri relativi manca il reciproco. Se l'estensione N→Z e Z→Q sono motivate quindi da esigenze di carattere algebrico, diverso è il carattere dell'estensione Z→R. Consideriamo un problema geometrico. La retta non viene definita direttamente, ma le sue proprietà risultano dai postulati, che noi possiamo ammettere, decidendo come vogliamo pensare sia fatta la retta. Se, per esempio costruiamo, a partire dall'origine, un quadrato di lato 1, ci si chiede il cerchio che ha per raggio la diagonale del quadrato, taglierà da qualche parte la retta. Non c'è dubbio che, andando dietro alla nostra intuizione, la risposta alla domanda sarà certamente "si".
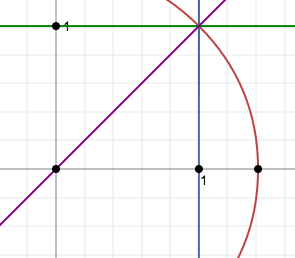
Infatti la diagonale del quadrato è √2, ma pensando che √2 non è un numero razionale, si deve ammettere che i punti di ascissa razionale non esauriscono la retta altrimenti dobbiamo ammettere che la retta stessa abbia un buco in √2. A tal proposito si può dimostrare facilmente che x2=2 non ha soluzioni nel campo dei numeri razionali. Quindi, bisogna supporre l'esistenza di nuovi enti e definirli, partendo dai numeri razionali e ritrovare, tra questi i numeri razionali stessi. Se nell'esempio precedente, la circonferenza non intersecasse la retta, l'insieme dei punti della retta potrebbe essere ripartito in due classi.
La prima classe conterrebbe i punti S a sinistra dello zero e quei punti S a destra dello zero tali che OS2<2OU2 con OU a rappresentare il segmento [0;1]. La seconda classe conterrebbe i punti D a destra dello zero tali che OD2>2OU2 con OU a rappresentare il segmento [0;1]. Ogni punto della retta troverebbe posto in una (e una sola) delle due classi, la prima sarebbe priva di massimo e la seconda sarebbe priva di minimo. Un numero reale sarà pensato come originato da una coppia di semirette razionali. Ci sono diversi modi di introdurre i numeri reali: quello delle coppie di classi contigue (Cantor), quello delle coppie di successioni convergenti, qui faremo riferimento a quello delle sezioni del campo razionale (Dedekind).
Sezioni del campo razionaleDiremo sezioni del campo razionale ogni coppia (S,D) di classi di numeri razionali che soddisfa le segurnti condizioni:
- nessuna delle due classi è vuota
- ogni numero di S è minore di ogni numero di D
- S non ha massimo, D non ha minimo
- se s∈S ∧ se s' < s, →s'∈S, se d∈D, ∧ d'>d →d'∈D
- ogni numero razionale, escluso al più uno, sta in S oppure in D.
Si distingueranno le sezioni di prima specie, quelle in cui c'è un numero razionale escluso da entrambe le classi e sezioni di seconda specie, quelle per le quali è S∪D=Q
Definizione: un numero reale è ogni sezione del campo razionale. L'insieme dei numeri reali si indicherà con R.
Con R+0 indicheremo l'insieme dei numeri reali positivi compreso lo zero
Con R-0 indicheremo l'insieme dei numeri reali negativi compreso lo zero
Con R+ indicheremo l'insieme dei numeri reali positivi escluso lo zero
Con R- indicheremo l'insieme dei numeri reali negativi escluso lo zero
Si vuole ora estendere la definizione di potenza al caso di esponente reale.
Per esempio √2 sarà rappresentato dalla sezione (S , D) con S = {Q- ∪ x∈Q+: x2<2} e D = {x∈Q+: x2>2}. All'insieme S appartengono numeri razionali come 1 , 1.4, 1.41, 1.414, … e all'insieme D appartengono numeri razionali come 2, 1.5, 1.42, 1.415, … Si tratta di una sezione di seconda specie. Dato b > 0 supponiamo di associare alle classi S, D dell’esempio le classi: H={h∈Q: h=bx x∈S}, K={k∈Q: k=bx x∈D}. All'insieme H appartengono numeri razionali come b 1, b 1.4, b 1.41, b 1.414, … All'insieme K appartengono numeri razionali come b 2, b 1.5, b 1.42, b 1.415, … Allora è naturale pensare che a√2 sarà rappresentato dalla sezione ( H , K ). Si dà allora la seguente definizione:
Definizione: si definisce potenza del numero reale positivo a con esponente reale w il numero reale positivo aw definito dalla sezione costituite dalle potenze di a che hanno per esponenti i numeri appartenenti alle due classi che definiscono l’esponente k.
Grafici
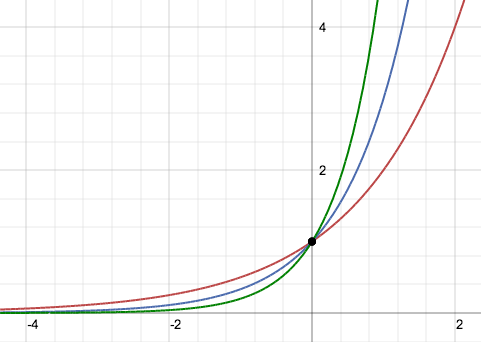
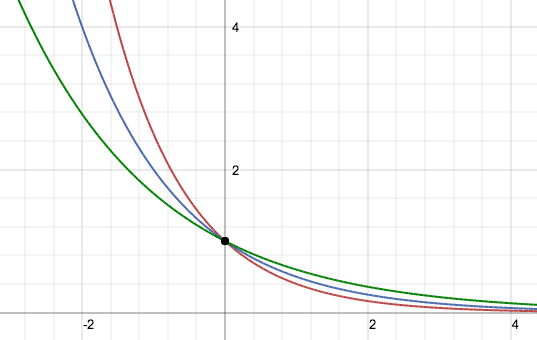
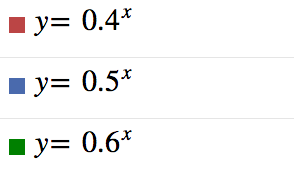
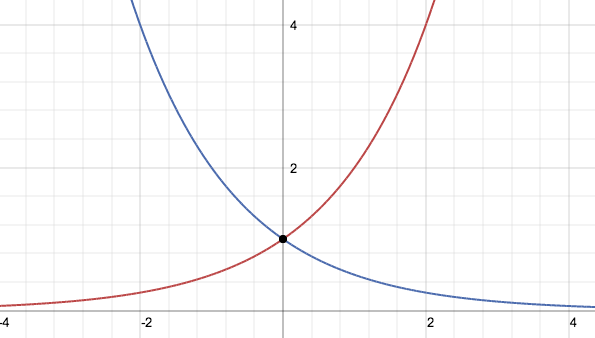
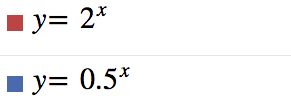
Equazioni esponenziali
Un'equazione è da considerarsi esponenziale se presenta almeno una potenza che abbia l'incognita nel proprio esponente.
Le equazioni esponenziali possono presentarsi sotto diverse forme per cui non esiste un metodo generale per la loro risoluzione, si daranno alcune indicazioni di carattere generale e si analizzeranno solamente dei casi particolari.
L'equazione esponenziale più semplice che possiamo scrivere è la seguente: bx=a con b>0. Valutiamo che cosa può succedere in questo caso
Se l'equazione proposta è del tipo bx=a con a<0 allora l'quazione è impossibile poichè bx è sempre positivo per qualsiasi valore attrbuito alla variabile x.
Se l'equazione proposta è del tipo 1x=a con a diverso da uno allora l'equazione è impossibile poichè 1x è sempre uguale a uno per qualsiasi valore attribuito alla variabile x.
L'equazione 1x=1 è indeterminata in quanto è soddisfatta per ogni valore attribuito alla variabile x.
Se a e b sono positivi e si riescono a scrivere come potenze della stessa base allora l'equazione sara determinata e potrà essere risolta con semplici passaggi per esempio: 9x=81 → 32x=34 da cui, siccome le basi sono uguali possiamo scrivere che gli esponenti sono uguali: 2x=4 → x=2.
- Se a e b non si riescono a scrivere come potenze della stessa base allora, dopo aver controllato che le due basi assumono valori positivi, si può trasformare l'equazione applicando un logaritmo nella stessa base ad entrambi i membri per esempio: 2*3x=5 applichiamo il logaritmo in base 10 → log(2*3x)=log5 da cui, applicando la prima proprietà: log2+log3x=log5 trasportando log2 al secondo membro si ottiene: log3x=log5-log2 applicando la quarta proprietà xlog3=log5-log2 ed infine dividendo entrambi i membri per log3 si ottiene la soluzione x=(log5-log2)/log3.
Applicando il logaritmo e le sue proprietà si possono risolvere quindi equazioni esponenziali che non presentano basi uguali. Per la risoluzione di altri casi particolari di funzioni esponenziali si rimanda alla parte esercizi.