Dati statistici
Costruire la tabella di distribuzione a doppia entrata lanciando 30 volte due dadi considerando la frequenza della somma dei valori usciti.
| dado rosso | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| d a d o b i a n c o | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 7 |
| 2 | -- | -- | 1 | -- | 1 | 1 | 3 | |
| 3 | 1 | 2 | -- | 2 | 1 | -- | 6 | |
| 4 | 1 | 1 | 1 | 1 | -- | 1 | 5 | |
| 5 | 1 | 1 | 1 | -- | -- | 1 | 4 | |
| 6 | 1 | 2 | 1 | -- | -- | 1 | 5 | |
| 5 | 8 | 5 | 4 | 3 | 5 | 30 | ||
Si sono lanciati per 30 volte due dadi, uno bianco ed uno rosso e ogni volta si è preso nota delle varie uscite. E' stata costruita la tabella di sinistra per poter leggere ciò che si è verificato.
All'incrocio della terza riga con la quarta colonna si trova il numero due, ciò significa che su trenta lanci per due volte è uscito il quattro sul dado rosso ed il tre sul dado bianco. All'incrocio della quinta riga con la quinta colonna non c'è alcun risultato, ciò significa che su trenta lanci non è mai uscito contemporaneamente il cinque sia sul dado rosso che sul dado bianco. Alla fine di ogni riga c'è la somma che rappresenta le volte che è uscito il numero della riga sul dado bianco. Alla fine di ogni colonna c'è la somma che rappresenta le volte che è uscito il numero della riga sul dado rosso. Il trenta che si trova in basso a destra, nell'ultima cella, rappresenta la somma, sia in orizzontale, che in verticale del numero dei lanci.
| statura | frequenza | frequenza cumulata | frequenza relativa cumulata |
| 161 | 1 | 1 | 0,05 |
| 162 | 7 | 8 | 0,4 |
| 166 | 4 | 12 | 0,6 |
| 181 | 1 | 13 | 0,65 |
| 185 | 2 | 15 | 0,75 |
| 186 | 4 | 19 | 0,95 |
| 195 | 1 | 20 | 1 |
Dividere i seguenti dati 186, 195, 162, 162, 166, 186, 185, 161, 166, 186, 186, 181, 162, 162, 166, 162, 185, 162, 162, 166, che rappresentano le stature in cm di un'insieme di ragazzi in classi, quindi calcolare la frequenza, la frequenza cumulata e la frequenza relativa cumulata di ogni classe.
In tabella la risposta al problema. Si tratta di una tabella con quattro colonne. La prima colonna si è ottenuta scrivendo le classi di statura. La colonna della frequenza si è ottenuta contando il numero di studenti di una certa statura. La colonna della frequenza cumulata si è ottenuta facendo, in ogni cella, la somma dei numeri presenti nelle classi precedenti. La colonna della frequenza cumulata relativa si è ottenuta facendo, in ogni cella, il rapporto della relativa adiacente frequenza cumulata con 20 che è il numero totale di ragazzi ai quali è stata fatta la misurazione della statura.
-
Dividere i seguenti dati 1200, 1100, 1100, 1600, 1500, 1100, 1100, 1600, 1500, 1200, 1300, 1200, 1500, 1400, 1200, 1400, 1600, 1500, 1200, 1100, che rappresentano gli stipendi in euro dei dipendenti di una ditta in classi, quindi calcolare la frequenza, la frequenza cumulata e la frequenza relativa cumulata di ogni classe.
-
In un condominio abitano 20 famiglie. Un nucleo familiare è composto da 5 persone, 4 nuclei familiari sono composti da 4 persone, 11 nuclei familiari sono composti da 3 persone, 3 nuclei familiari sono composti da 2 persone, ed una persona abita da sola. Suddividere in classi i nuclei famigliari e calcolare la frequenza, la frequenza cumulata e la frequenza relativa cumulata di ogni classe.
-
Costruire la tabella di distribuzione a doppia entrata lanciando 40 volte due dadi considerando la frequenza della somma dei valori usciti.
-
Costruire la tabella di distribuzione a doppia entrata relativa ai compagni di classe in base al colore degli occhi ed al colore dei capelli.
-
Costruire la tabella di distribuzione a doppia entrata dei libri di testo in uso nelle varie materie in base al numero delle pagine ed in base al prezzo. Ripartire il numero delle pagine in classi di 50 ed il prezzo in classi di 8 euro.
Indici di posizione
Media aritmetica ponderata
| voto | crediti | punteggio ottenuto | punteggio massimo |
| 30 | 4 | 120 | 120 |
| 20 | 3 | 60 | 90 |
| 21 | 5 | 105 | 150 |
| 24 | 4 | 96 | 120 |
| 25 | 3 | 75 | 90 |
| 21 | 4 | 84 | 120 |
| totale | 23 | 540 | 690 |
Consideriamo la tabella a sinistra relativa ai voti di uno studente frequentante una certa facoltà universitaria. Come si può notare è previsto che ogni esame ha dei crediti. Facendo la somma di tutti otteniamo un totale di 23 crediti. Si moltiplica quindi il voto per il numero dei crediti ottenendo i valori della colonna 3. Il totale, facendo la somma è 540. Se lo studente avesse ottenuto sempre il massimo voto, ovvero 30, moltiplicandolo per i rispettivi crediti avrebbe ottenuto i prodotti indicati nella quarta colonna ed il totale sarebbe stato 690. Il voto x si calcola quindi con la proporzione x:30=540:690 da cui si ricava, semplificando, che x=540/23=23,47. Analizzando l'ultima formula scritta si può dire che il voto medio è dato dal rapporto tra la sommatoria dei prodotti dei voti per i rispettivi crediti fratto la sommatoria dei crediti stessi. Il voto poteva comunque essere calcolato, senza impostare la proporzione, con la media ponderata, applicando ad ogni singolo voto il giusto peso che è dato dal rapporto del singolo credito con il totale dei crediti.
Media aritmetica semplice
Un ciclista durante la prima ora va ad una velocità di a 30 km/h, la seconda ora mantiene una velocità di 20 km/h. Durante la prima ora ha percorso quindi 30 km, durante la seconda ora ha percorso 20 km. In totale i km percorsi sono 50. Dato che la velocità è data dal rapporto spazio/tempo la velocità media è 50/2 ovvero 25 km/h. La velocità media quindi, quando in tempi uguali si pedala a velocità differenti, si calcola tramite la media aritmetica.
Media geometrica
Esercizio 1
| anno | abitanti | delta | variazione | tasso |
| 2006 | 2134 | --- | --- | --- |
| 2007 | 2145 | 11 | 0,0051 | 1,0051 |
| 2008 | 2098 | -47 | -0,0219 | 0,9780 |
| 2009 | 2154 | 56 | 0,0266 | 1,0266 |
| 2010 | 2214 | 60 | 0,0278 | 1,0278 |
| 2011 | 2331 | 117 | 0,0528 | 1,0528 |
Consideriamo la tabella a sinistra relativa al numero di abitanti di un paese dal 2006 al 2011. Determiniamo la percentuale media di variazione della popolazione. Nel 2007 si è manifestato un incremento, rispetto all'anno precedente, di 11 unità cioè si è avuta una variazione percentuale: 11/2134=0,0051 del 0,51%. Eseguendo tutti i calcoli per gli altri anni otteniamo i risultati della tabella. Osserviamo che per passare dal numero di abitanti di un certo anno a quello dell'anno dopo dobbiamo moltiplicare il numero di abitanti per il tasso. Il tasso si determina sommando alla variazione il numero 1. Si noti che il tasso di variazione non è niente altro che il rapporto tra gli abitanti di un anno e quelli dell'anno precedente. Moltiplicando quindi il numero di abitanti del 2006 per il primo tasso di incremento troviamo il numero di abitanti del 2007, se poi questo numero lo moltiplichiamo per i tassi sucessivi fino all'ultimo, troviamo il numero degli abitanti dell'anno 2011.
Quindi 2134 • 1,0051• 0,978 • 1,0266 • 1,0278 • 1,0528 = 2331. Cerchiamo ora un valore t tale che: 2134 • t • t • t • t • t = 2134 • t5 = 2331. Tale valore è chiamato tasso medio di variazione. Quindi t5=2331/2134 ovvero t5=2134 • (1,0051• 0,978 • 1,0266 • 1,0278 • 1,0528)/2134. Semplificando t5=(1,0051• 0,978 • 1,0266 • 1,0278 • 1,0528). Il tasso di variazione sarà dato quindi, nel nostro caso, dalla radice quinta del prodotto dei singoli tassi di incremento. In questo caso la media Geometrica rappresenta il tasso medio di incremento.
Esercizio 2
| anno | rendimento | tasso | capitale |
| I | 0,7% | 1,007 | 10070 |
| II | 0,7% | 1,007 | 10140,49 |
| III | 0,8% | 1,008 | 10221,61 |
| IV | 0,8% | 1,008 | 10303,38 |
| V | 0,9% | 1,009 | 10396,11 |
| VI | 0,9% | 1,009 | 10489,68 |
| VII | 0,9% | 1,009 | 10584,08 |
Un capitale di €10000 è stato vincolato per 7 anni in un deposito a risparmio avendo avuto i rendimenti indicati in tabella. Si vuolr calcolare l'aumento percentuale medio. Per prima cosa si calcolerà il tasso annuale che permette di passare dal capitale di un anno a quello dell'anno successivo.
Per i primi due anni il tasso si calcola sommando ad uno il rendimento diviso per 100 quindi, poichè il rendimento è del 0,7% diviso 100 fa 0,007, il è 1+0,007 ovvero 1,007.
Il rendimento del terzo e quarto anno è del 0,8% diviso 100 fa 0,008, il tasso è 1+0,008 ovvero 1,008.
Il rendimento degli ultimi tre anni è del 0,9% diviso 100 fa 0,009, il tasso è 1+0,009 ovvero 1,009.
A questo punto va calcolata la media geometrica facendo la radice settima del prodotto dei sette tassi.
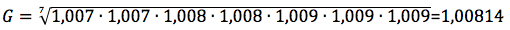
La media Geometrica rappresenta il tasso medio, che è 1,00814, per calcolare l'aumento percentuale medio da questo valore bisogna togliere uno ottenendo 0,00814, infine moltiplicando per cento questo valore si ottiene 0,814 che è proprio il rendimento percentuale medio.
Media armonica ponderata
Supponiamo ora che un ciclista percorra 12 km a 30 km/h, 9km a 20 km/h e 6 km a 15 km/h, in questo caso notiamo che gli spazi percorsi non sono uguali. Possiamo allora suddividere il percorso in intervalli più piccoli facendo il massimo comun divisore dei tre valori 12, 9, 6, che è 3.
| velocità | tratti |
| 30 | 4 |
| 20 | 3 |
| 15 | 2 |
Possiamo allora immaginare che, nel problema proposto, il ciclista abbia percorso 4 intervalli di 3 km a 30 km/h, 3 intervalli a 20 km/h e 2 intervalli a 15 km/h. In totale ha percorso 9 intervalli uguali di spazio. Anche in questo caso si calcola la velocità media con la stessa formula di sopra che con le opportune semplificazioni diventa:
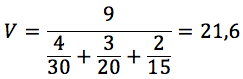
Media armonica
Esercizio 1
| litri di benzina acquistati | ||
| tempo | prezzo | litri |
| I | 1,48 | 33,78 |
| II | 1,54 | 32,47 |
| III | 1,56 | 32,05 |
| totale litri | 98,30 | |
Nella tabella, è indicato il prezzo della benzina i tre diversi periodi. In ognuno di questi tre periodi si è fatto un rifornimento di 50 euro. Si vuol calcolare qual'è stato il costo medio di un litro di benzina. Dobbiamo calcolare quanti litri di benzina abbiamo acquistato ogni volta che ci siamo riforniti, dividendo i 50 euro per il prezzo al litro.
Otteniamo i valori presenti nella terza colonna. In totale sono si sono spesi 150 euro acquistando 98,3 litri di benzina, quindi il costo di un litro di benzina e' dato da:
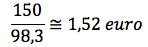
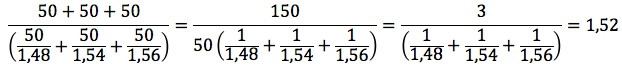
Esercizio 2
Un ciclista percorre 10 km a 30 km/h sucessivamente altri 10 km a 20 km/h. Si vuol calcolare la velocità media. La velocità si calcola mediante il rapporto spazio/tempo, nel nostro caso lo spazio totale e' dato dalla somma di 10 km + 10 km ovvero 20 km. Il tempo totale di percorrenza T sarà dato dalla somma T=T1+T2 , dove T1 è il tempo impiegato nel percorrere i primi 10 km e T2 è il tempo impiegato nel percorrere gli altri 10 km. Il tempo, per la formula inversa, si calcola mediante il rapporto spazio/velocità, quindi siccome T1=S1/V1 e T2=S2/V2, la velocità media si calcola quindi mediante la formula:
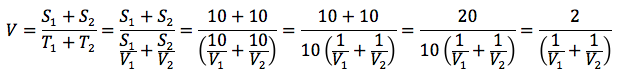
Sostituendo i valori dati, 30 e 20 si ottiene che la velocita' media e' di 24 km/h.
Più in generale, se percorriamo n spazi uguali con velocita' V1 V2 V3 ... Vn, la velocità media si calcola con la seguente formula:
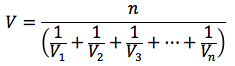
La velocità media quindi, quando si percorrono spazi uguali a velocità differenti, si calcola tramite la media arimonica.
Media quadratica semplice
Un orefice ha cinque medaglie d'oro tutte dello stesso spessore e con raggi differenti. Deve fonderle per ricavare, con lo stesso materiale, altre cinque medaglie, tutte uguali e dello stesso spessore delle precedenti. Le cinque medaglie hanno rispettivamente raggio in mm uguale a 4, 6, 8, 11, 12. Calcoliamo quale è il raggio delle nuove medaglie.
La superficie delle cinque medaglie è rispettivamente S1=Π42, S2=Π62, S3=Π82, S4=Π112, S5=Π122. L'area totale sarà quindi: S=S1+S2+S3+S4+S5, ovvero raccogliendo Π, S=Π(42+62+82+112+122). Per calcolare la superfice della singola medaglia si divide questo valore per 5. Per trovare il raggio delle nuove monete, con la formula inversa dovremo dividere la superficie totale per Π e fare la radice. Otterremo quindi
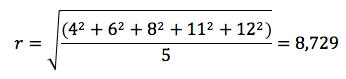
Media quadratica ponderata
| raggio | spessore | peso |
| 6 | 0,8 | 4 |
| 4 | 0,4 | 2 |
| 5 | 0,6 | 3 |
Un orefice ha tre medaglie d'oro con spessore e raggi differenti come indicato in tabella. Deve fonderle per ricavare, con lo stesso materiale, altre nove medaglie, tutte uguali tra loro e tutte di spessore 0,2 mm. Possiamo allora pensare a creare medaglie tutte di 0,2 mm di spessore. Quindi, nel problema proposto, avremo quattro medaglie di raggio 6, due medaglie di raggio 4 e tre medaglia di raggio 5, tutte dello stesso spessore. Il "peso" della medaglia di raggio 6 risulta pertanto 4 ecc.. come indicato in tabella, quindi sarebbe come avere non tre, ma nove medaglie però tutte dello stesso spessore. Il raggio delle nove medagli tutte uguali tra di loro si calcolerà quindi mediante la seguente formula:
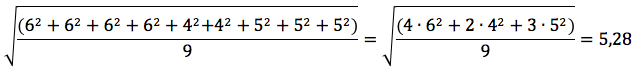
-
Calcolare la velocità media di un veicolo che percorre 20 km a 80 km/h, e 20 km a 100 km/h.
-
Calcolare la velocità media di una persona che nuota 10 vasche a 2,2 km/h e altre 10 vasche a 1,6 km/h.
-
Un'auto di formula 1 percorre mezzo granpremio a 210 km/h e l'altro mezzo granpremio a 190 km/h. Calcolare la velocità media con cui ha percorso l'intero granpremio.
-
Calcolare la velocità media di un veicolo che percorre 15 km a 60 km/h, 5km a 120 km/h e 25 km a 70 km/h.
-
Calcolare la media della seguente serie di numeri: 2, 4, 7, 11, 18, con le rispettive frequenze: 3, 2, 3, 1, 4.
9,069
Calcolare la media della seguente serie di numeri: 3, 6, 8, 12, 19, 26 con le rispettive frequenze: 3, 2, 3, 1, 4, 2.
-
Calcolare la moda e mediana della seguente serie di numeri: 12, 6, 12, 15, 6, 1, 12, 19, 7, 7, 22.
-
Calcolare la moda e mediana della seguente serie di numeri: 12, 6, 10, 12, 19, 8, 8, 23.
-
Calcolare la moda e mediana della seguente serie di numeri: 12, 6, 9, 12, 19, 8.
-
Calcolare la moda e mediana della seguente serie di numeri: 11, 7, 9, 23, 18.
-
Calcolare le medie ponderate della seguente serie di numeri: 3, 5, 5, 6, 7, 8, 5, 6, 9.
Mp=6; Ap=5,45 Gp=5,74 Qp=6,23
-
Due tubi con diametro rispettivo di 6cm e 8cm confluiscono in un nodo dal quale partono altri due tubi che devono avere lo stesso diametro. Siccome questi tubi devono far scorrere la stessa quantità di acqua, calcolare quale dev'essere il diametro che questi due tubi devono avere.
9,06
-
Calcolare la velocità media di un automobile che percorre 2km a 30km/h, 12km a 60km/h e 20km a 100km/h.
72,86km/h
-
Due quadrati aventi i lati di 8 m e 10 m devono essere sostituiti da altri due quadrati, in modo che la superfice totale rimanga la stessa. Calcolare quale dev'essere la misura del lato dei due nuovi quadrati.
-
Nella tabella seguente è riportato il numero di abitanti di un paerse dall'anno 2000 all'anno 2010. Determinare il tasso medio di variazione della popolazione.
anno 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 abitanti 12345 12312 12356 12400 12410 12421 12458 12523 12589 12670 12765 -
Un paese ha 9000 abitanti. Dopo 4 anni la popolazine è di 11115 abitanti. Determinare il tasso annuale medio di variazione della popolazione ed in base a questo determinare il numero di abitanti che dovrebbero esserci alla fine del secondo anno.
100002
Indici di dispersione
Varianza
| studente A | |||
| voti | scarti | scarti2 | |
| 7 | -1,4 | 1,96 | |
| 6 | -0,4 | 0,16 | |
| 4 | 1,6 | 2,56 | |
| 5 | 0,6 | 0,36 | |
| 6 | -0,4 | 0,16 | |
| media | 5,6 | ||
| scarto quadratico medio | 1,0198 | ||
| varianza | 1,04 | ||
| studente B | |||
| voti | scarti | scarti2 | |
| 8 | -2,4 | 5,76 | |
| 7 | -1,4 | 1,96 | |
| 4 | 1,6 | 2,56 | |
| 2 | 3,6 | 13 | |
| 7 | -1,4 | 1,96 | |
| media | 5,6 | ||
| scarto quadratico medio | 2,2449 | ||
| varianza | 5,04 | ||
Nelle due tabelle precisamente nella prima colonna, sono riportati i voti meritati da due studenti in una certa materia. E' stata calcolata la media che in entrambi i casi è 5,6. Quale dei due studenti risulta più preparato?
Nella seconda colonna sono stati calcolati gli scarti dalla media e nella terza colonna i relativi quadrati. E' stata calcolata quindi la varianza eseguendo la media degli scarti elevati al quadrato e, con la radice quadrata della varianza è stato calcolato lo scarto quadratico medio.
A questo punto traiamo le conclusioni dicendo che lo studente A avendo una varianza minore avrà una preparazione più uniforme. Lo studente B meriterà sicuramente il voto 5 in pagella.
Gaussiana
In uno stato di 1245000 abitanti la statura media è di 178 cm lo scarto quadratico medio σ=4 cm. Sapendo che la misurazione ha una distribuzione gaussiana, determinare:
1. quante persone hanno statura superiore a 174 cm.
2. quante persone hanno statura superiore a 189 cm.
Per rispondere alla prima domanda, si osservi che 174=178-σ e tenendo presente che in una distribuzione gaussiana nell'intervallo tra:
[x media-σ , x media+σ] cade il 68.7% della popolazione
[x media-2 σ , x media+2 σ] cade il 95.45% della popolazione
[x media-3 σ , x media+3 σ] cade il 99.735% della popolazione
le persone di statura superiore a 174 cm saranno il 50% della popolazione sommato alla metà del 68,27% cioè 84,135%. Eseguendo i calcoli 1245000*0,84135=1047480 persone.
Per rispondere alla seconda domanda, si osservi che 170=178-2σ e 182=178+σ si dovrà calcolare quindi, la metà del 95,45% sommata alla metà del 68,27% ovvero (95,45/2)+(68,27/2)=81,86. Eseguendo i calcoli 1245000*0,8186=1019157 persone hanno statura compresa tre 170 cm e 182 cm.
Concentrazione
In una ditta, i giorni di assenza in un anno, con durata massima di una settimna sono così distribuiti: 1 giorno di assenza 22 casi, 2 giorni 11 casi, 3 giorni 25 casi, 4 giorni 9 casi, 5 giorni 7 casi, 6 giorni 4 casi. Costruire l'area di concentrazione e calcolare l'indice di concentrazione
| giorni assenza | numero casi | intensità | frequenza cumumulata | intensità cumulata | frequenza relativa cumulata | intensità relativa cumulata | area trapezi |
| 1 | 22 | 22 | 22 | 22 | 0,28 | 0,10 | 0,01 |
| 2 | 11 | 22 | 33 | 44 | 0,42 | 0,21 | 0,02 |
| 3 | 25 | 75 | 58 | 119 | 0,74 | 0,56 | 0,12 |
| 4 | 9 | 36 | 67 | 155 | 0,86 | 0,72 | 0,07 |
| 5 | 7 | 35 | 74 | 190 | 0,95 | 0,89 | 0,07 |
| 6 | 4 | 24 | 78 | 214 | 1 | 1 | 0,05 |
somma aree trapezi | 0,3529 | ||||||
area concentrazione=area di massima concentrazione-somma aree trapezi | 0,147 | ||||||
indice di concentrazione=area di concentrazione/area di massima concentrazione | 0,2941 | ||||||
percentuale dell'area di massima concentrazione occupata dall'area di concentrazione | 29,41% | ||||||
Calcolo automatico dell'indice di concentrazione
| valore centrale | frequenza | intensità | frequenza cumulata | intensità cumulata | frequenza relativa cumulata | intensità relativa cumulata | area trapezi |
somma aree trapezi | |||||||
area concentrazione=area di massima concentrazione-somma aree trapezi | |||||||
indice di concentrazione=area di concentrazione/area di massima concentrazione | |||||||
percentuale dell'area di massima concentrazione occupata dall'area di concentrazione | |||||||
Coefficiente di variazione
| mese | Italia | Slovenia |
| febbraio | 1,56 | 1,44 |
| marzo | 1,55 | 1,52 |
| aprile | 1,52 | 1,45 |
| maggio | 1,62 | 1,46 |
| giugno | 1,66 | 1,48 |
Nella tabella è indicato il prezzo della benzina in euro rilevato in 5 mesi successivi in Italia ed in Slovenia. Determinare il coefficiente di variazione del prezzo della benzina in entrambi gli stati per farne un confronto. Siccome il coefficiente di variazione è dato dal rapporto tra lo scarto quadratico medio σ e la media, in valore assoluto, è necessario innanzitutto calcolare la media. Sucessivamente vanno calcolati gli scarti dalla media che poi devono essere elevati al quadrato. Va fatta quindi la media degli scarti al quadrato ed della media degli scarti elevati al quadrato si esegue la radice quadrata per determinare lo scarto quadratico medio.
| Italia | |||
| mese | prezzo | scarti | scarti al quadrato |
| febbraio | 1,56 | 0,022 | 0,000484 |
| marzo | 1,55 | 0,032 | 0,001024 |
| aprile | 1,52 | 0,062 | 0,003844 |
| maggio | 1,62 | -0,038 | 0,001444 |
| giugno | 1,66 | -0,078 | 0,006084 |
| media | 1,582 | ||
| scarto quadratico medio | 0,050 | ||
| coefficiente di variazione | 0,032 | ||
| Slovenia | |||
| mese | prezzo | scarti | scarti al quadrato |
| febbraio | 1,44 | 0,03 | 0,0009 |
| marzo | 1,52 | -0,05 | 0,0025 |
| aprile | 1,45 | 0,02 | 0,0004 |
| maggio | 1,46 | 0,01 | 0,0001 |
| giugno | 1,48 | -0,01 | 0,0001 |
| media | 1,47 | ||
| scarto quadratico medio | 0,028 | ||
| coefficiente di variazione | 0,019 | ||
Infine si esegue il rapporto tra scarto quadratico medio e la media, in valore assoluto, per determinare il coefficiente di variazione. Nelle due tabelle di sopra, troviamo l'indicazione dei valori ottenuti. Tutti questi calcoli sono stati fatti per confrontare, attraverso il coefficiente di variazione, la variabilità dei prezzi della benzina in due stati confinanti come lo sono Italia e Slovenia. Si può notare quindi, in conclusione, che il prezzo della benzina in Italia ha una variabilità più elevata rispetto a quello rilevato, in cinque masi sucessivi, in Slovenia.
-
In una popolazione di 15450000 abitanti la statura media è di 177 cm e lo scarto quadratico medio σ = 4 cm. Sapendo che la misurazione ha una distribuzione gaussiana, determinare quante persone hanno statura superiore a 173 cm quante persone hanno statura compresa tra 169 cm e 181 cm e quante persone hanno statura superiore a 189 cm.
[12998858, 12647370, 2085750]
-
In una popolazione di 10000000 abitanti la statura media è di 175 cm e lo scarto quadratico medio σ = 5 cm. Sapendo che la misurazione ha una distribuzione gaussiana, determinare quante persone hanno statura superiore a 185 cm, quante persone hanno statura compresa tre 165 cm e 170 cm e quante persone hanno statura compresa tre 170 cm e 175 cm.
[228000, 1359000, 3413500]
-
Calcolare lo scarto quadratico medio e la varianza della seguente serie di dati: 9, 5, 6, 6, 7, 5, 8.
[σ=1,4,σ2=1,96]
-
Calcolare lo scarto quadratico medio e la varianza della seguente serie di dati: 10, 4, 8, 7, 6, 5, 9.
[σ=2,σ2=4]
-
Calcolare il coefficiente di variazione della seguente serie di dati: 28, 27, 18, 22, 30, 23, 23.
-
Nelle tabelle sono riportati gli stipendi percepiti dai dipendenti di tre ditte suddivisi in classi stipendiali. Ogni ditta è composta da 20 dipendenti con gli stipendi ripartiti 6 classi. Nelle tabelle con n si è indicato il numero di impiegati per classe stipendiale. Costruire l'area di concentrazione e calcolare l'indice di concentrazione nei tre casi.
classe stipendio n max min I 800 900 2 II 900 1100 2 III 1100 1300 5 IV 1300 1600 7 V 1600 1900 2 VI 1900 2100 2 classe stipendio n max min I 900 1100 1 II 1100 1200 4 III 1200 1300 5 IV 1300 1400 5 V 1400 1600 2 VI 1600 2100 3 classe stipendio n max min I 900 1000 1 II 1000 1100 3 III 1100 1300 5 IV 1300 1600 8 V 1600 1900 2 VI 1900 2300 1