Equazioni e sistemi
Esercizio 1
Risolviamo un' equazione di primo grado in Z5
3x+4=x+2 sommiamo l'opposto di 4 che è 1 ad entrambi i membri ... primo principio di equivalenza delle equazioni ... otteniamo:
3x+4+1=x+2+1 da cui otteniamo
3x=x+3 l'effetto è quello di avere, al primo membro solamente termini contenenti l'incognita x, sommiamo l'opposto di x che è 4x ad entrambi i membri ... primo principio di equivalenza delle equazioni ... otteniamo:
3x+4x=x+3+4x otteniamo: 2x=3 l'effetto è quello di avere, al secondo membro solamente termini noti,
moltiplichiamo entrambi i membri per il reciproco di 2 che è 3 ... secondo principio di equivalenza delle equazioni ... otteniamo:
x=4 che è la soluzione
verifica: 3*4+4=4+2 ... 2+4=4+2 ... 1=1
Esercizio 2
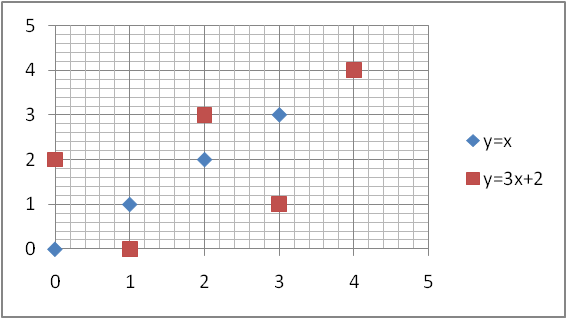
Risolviamo un sistema di primo grado in Z5 costituito dalle due equazioni di sotto.
y=x
Y=3x+2
Risolviamo il sistema per sostituzione:
x=3x+2 aggiungo 2x: 2x+x=3x+2+2x otteniamo: 3x=2 moltiplichiamo per 2: x=4 risostituendo: y=4, la soluzione è: (4,4).
In figura la soluzione grafica.
Risolviamo un' equazione di secondo grado in R(+,*)
x2+2x+4=0Δ=b2-4ac
Δ=22-4*1*4 =-8 impossibile
Risolviamo l'equazione x2+2x+4=0
in Z7 Δ=b2-4ac
Δ=22-4*1*4=4-16=-12=2 infatti -12≡-5 e -5≡2
x1,2= (-b±√Δ)/2a
x1,2=(-2±√2)/(2*1) Notiamo che, in Z7 non c'è il numero -2, ma se andiamo, rispetto all'ora zero, indietro di due ore allora troviamo l'ora 5, cioè il numero -2 equivale al cinque. Come fare la radice quadrata di 2? Bisogna determinare quel numero che elevato al quadrato dà due. Il numero cercato è 3 perche 32=9, che è equivalente a due.
x1=(5+3)/2=1/2 il numero 1/2 equivale al reciproco di 2 che in Z7=4, quindi x1=4, x2=(5-3)/2=2/2=1.
Verifica:
con x1=4
42 + 2*4+4=0, 16+8+4=0, 2+1+4=0, 7 = 0
con x2=1, 122+2*1+4=0, 1+2+4=7, 7=0
Risolviamo un'equazione di secondo grado in Z8
x2+2x+4=0
In Z8 non c'è reciproco per ogni elemento quindi non si possono determinare le soluzioni usando il reciproco. Allora come si procede? Visto che in Z8 ci sono solo 8 elementi si fanno 8 verifiche: e si nota che l'equazione è impossibile. Sempre in Z8 un'equazione potrebbe avere anche più di due soluzioni come si può notare dall'esempio: x2+2x=0 anche in questo caso non essendo 8 un numero primo si fanno 8 verifiche e si nota che ci sono ben 4 soluzioni: 0, 2, 4, 6.
Quindi quando risolviamo equazioni in Zn se n non è numero primo non c'è reciproco e possono succedere delle stranezze rispetto alle equazioni che hanno soluzioni in R che ha la struttura di campo. Quando invece n è numero primo la struttura algebrica è quella di campo e il numero massimo di soluzioni corrisponde al grado dell'equazione stessa.
Risolviamo un sistema di secondo grado in Z7 costituito dalle due equazioni di sotto.
y=2x
y=x2+3x+5
Risolviamo il sistema per sostituzione:
x2+3x+5=2x sommiamo 5x: x2+x+5=0
Δ=1-4*5=1+3*5=16 ≡ 2
x1,2=(-1±√2)/2
x1=2/2=1 y1=2*1=2
x2=(6+4)/2=5 y2=2*5=3
quindi ci sono le due soluzioni (1,2) e (5,3).
In figura la soluzione grafica.
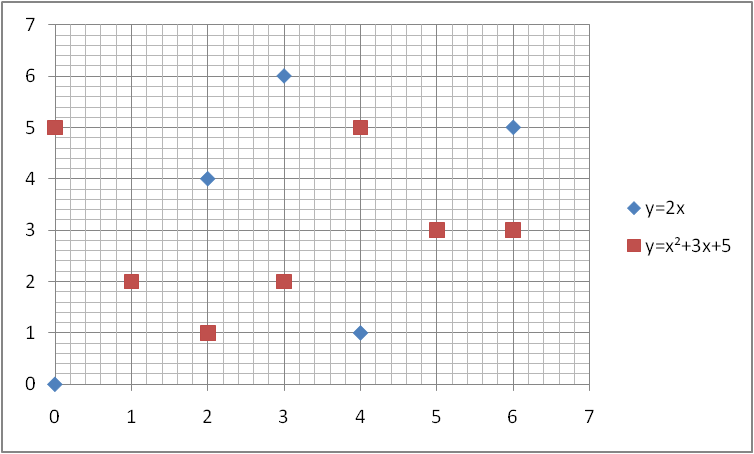
Si noti che le soluzioni della prima è l'insieme delle coppie ordinate: (0,0), (1,2), 2,4), (3,6), (4,1), (5,3), (6,5), le soluzioni della seconda: (0,5), (1,2), (2,1), (3,2), (4,5), (5,3), (6,3), le coppie (1,2) e (5,3), che appartengono all'intersezione, costituiscono quindi le soluzioni del sistema.
In Z11, risolvere l'equazione 2x+9=3x+3.
In Z5, risolvere l'equazione 2x+2=x+3.
[1]In Z11, risolvere l'equazione x2+2x+9=0.
[4,5]In Z7, risolvere l'equazione x2+2x+2=0.
In Z8, risolvere l' equazione: 2x+2=0, tenendo conto che 8 non è numero primo.
[3,7]In Z7, risolvere, sia analiticamente che graficamente il sistema composto dalle seguenti equazioni: y=2x+1, y=5x+3.
[(1,3)]In Z5, risolvere, sia analiticamente che graficamente il sistema composto dalle seguenti equazioni: y= x2+1, y=2x+3.
[sistema impossibile]
Funzioni
Disegnare il grafico della funzione y = f(x) =x2+2x+6 in Z7, intendendo che le operazioni sono in modulo 7. Si calcolano i sette valori che la funzione assume rispettivamente in 0,1,2,3,4,5,6, ne viene il grafico illustrato dalla figura che mostra una parabola in modulo 7.
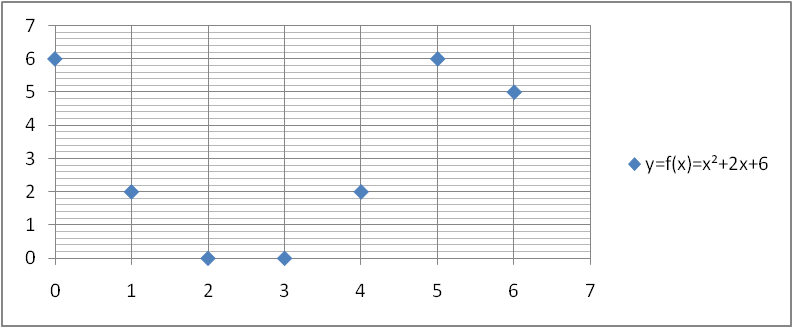
Si noti che la funzione f non è iniettiva perchè sulle due orizzontali y=3, y=4 non c'è neanche un punto.
Si noti che la funzione f non è suriettiva perchè sulle tre orizzontali y=0, y=2 e y=6 ci sono due punti.
Sia y= f(x)= 2x + 2
f(x), funzione di R → R. Determinare la funzione inversa.
La f è una retta obliqua e quindi funzione biettiva e quindi invertibile. Per scrivere l'espressione della funzione inversa va esplicitata la variabile x, quindi si rinominano le variabili per cui x lo chiamiamo y e y lo chiamiamo x, questo affinchè l'asse delle ascisse sia sempre l'asse x. Esprimendo la f a parole sarebbe fai il doppio e aggiungi due. Per l'inversa dovremo leggerla al contrario eseguendo le operazioni inverse: togli due e il risultato ottenuto dividilo per due.
y = 2x + 2 / -2
y - 2 = 2x / :2
(1/2)y - 1 = x
rinomino e quindi l'espressione trovata è:
y = (1/2)x - 1 da cui
y = i(x) = (x-2)/2.
Come si può vedere dal grafico
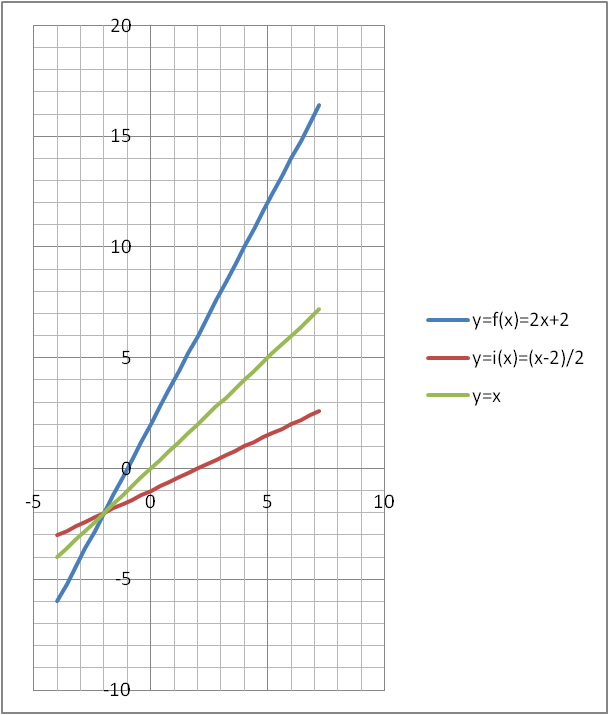
la f(x) e la i(x) sono simmetriche rispetto alla retta y = x.
Consideriamo la funzione y= f(x)= 2x + 2 in Z7:
Determinare l'inversa.
f(x), funzione di Z7 → Z7
Partiamo dalla funzione inversa ricavata in R: y = i(x) = (x-2)/2. In Z7, -2 equivale a 5 e ½ si interpreta come reciproco di 2 cioè 4, quindi ...y=(x-2)/2 → y=(x+5)/2 → y=(x+5)*4 → ... y= i(x)=4x+20 → y=i(x)=4x+6. Le due funzioni f, i sono due particolari rette costituite ciascuna da 7 punti, sono simmetriche rispetto alla retta y=x, come si nota nel grafico.
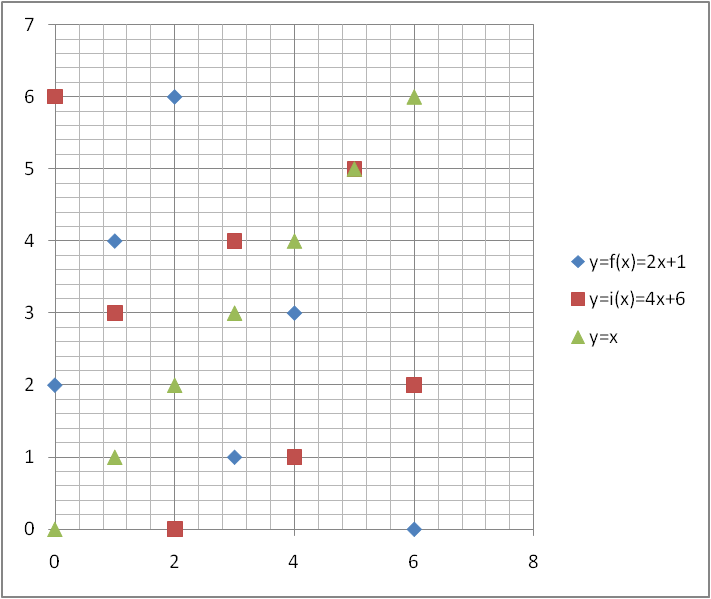
Si noti che la funzione f è iniettiva perchè su ogni orizzontale c'è al massimo un punto.
Si noti che la funzione f è suriettiva perche su ogni orizzontale c'è almeno un punto.
Si noti che la funzione f è biettiva perchè contemporaneamente iniettiva e suriettiva ovvero perchè su ogni orizzontale si trova un solo punto.
Le uniche funzioni invertibili sono quelle biettive ovvero quelle che presentano, su ogni orizzontale, un solo punto.
In Z7, disegnare il grafico della funzione y=3x+3.
In Z7, disegnare il grafico della inversa della funzione y=x+6.
In Z7, individuare funzioni involutorie (inverse di se stesse).
In Z11, disegnare il grafico della funzione y=x2+1.
In Z7, dopo aver disegnato il grafico della funzione y=2x+1, spiegare perchè è biettiva, determinare l'espressione analitica della funzione inversa e sullo stesso sistema di riferimento disegnare il grafico della funzione inversa, trovare quindi analiticamente il punto in comune alle due funzioni.
In Z7, dopo aver disegnato il grafico della funzione y=4x+2, spiegare perchè è biettiva, determinare l'espressione analitica della funzione inversa e sullo stesso sistema di riferimento disegnare il grafico della funzione inversa, quindi analiticamente determinare il punto in comune alle due funzioni.
[(4,4)]