Calcolo proposizionale
Conveniamo di assumere come primitivo il concetto di proposizione limitandoci a precisare che le proposizioni che d'ora in poi considereremo saranno affermazioni per le quali sia possibile stabilire senza ambiguità se sia vera o falsa.
Il concetto di proposizione
Ad ogni proposizione potremo dunque associare un valore di verità "vero" o "falso".
Ad esempio, sono proposizioni le seguenti frasi:
Roma è capitale d'Italia. - vero
L'aquila è un rapace. - vero
Il sette è un numero pari. - falso
Non sono invece proposizioni le frasi del tipo:
Che giorno è oggi?
Che bel libro!
Quell'automobile ha tre fiumi.
Il numero sei è calvo.
Il basket è il più bello degli sport.
Laura è simpatica.
Ossia non sono proposizioni le domande, le esclamazioni, le frasi senza senso, i giudizi soggettivi poichè ad espressioni di questo tipo non si può attribuire univocamente uno dei due valori di verità: "vero" o "falso"
Proposizioni atomiche e molecolari
Consideriamo le seguenti proposizioni:
1. il cane ha quattro zampe
2. la pioggia bagna la terra
3. l'anguilla è un pesce e il falco vola
4. il 4 è pari oppure il -7 è negativo
5. se ABC è un triangolo equilatero, allora ABC ha gli angoli uguali
Osserviamo che le proposizioni 1 e 2 non si possono scomporre in altre proposizioni più semplici, per le quali abbia ancora senso parlare di vero o falso, per questo motivo sono chiamate atomiche. Le proposizioni 3, 4, 5 invece sono scomponibili in proposizioni elementari in corrispondenza delle qualisi può ancora attribuire un ben determinato valore di verità. Infatti si ha che la 3 è composta dalle due proposizioni atomiche "l'anguilla è un pesce" e "il falco vola" collegate dalla congiunzione "e". La 4 è composta dalle due proposizioni "il 4 è pari", e "il -7 è negativo" collegate dalla disgiunzione "oppure". La 5 è composta dalle due proposizioni atomiche "ABC è un triangolo equilatero" e "ABC ha gli angoli uguali" collegati tramite l'implicazione "se... allora". Tutte queste proposizioni, che sono composte da due o più proposizioni atomiche si chiamano proposizioni molecolari.
Principi della logica
La logica delle proposizioni è fondata sui tre principi della logica Aristotelica:
Identità: ogni oggetto del pensiero logico è uguale a se stesso e a nessun altro oggetto.
Non contraddizione: una stessa proposizione non può essere contemporaneamente sia vera che falsa.
Terzo escluso: i valori di verità che può assumere una proposizione sono soltanto due, il vero oppure il falso, non esiste un terzo valore di verità.
Operazioni nell'insieme delle proposizioni
Ci si propone di definire, nell'insieme di tutte le proposizioni logiche, opportune operazioni di composizioni binarie ed interne che, applicate ad una coppia ordinata di proposizioni (P1, P2), diano come risultato una nuova proposizione del tipo seguente P=P1*P2, ottenibile con le modalità prescritte dall'operatore * chiamato operatore logico o connettivo logico.
Le operazioni che si possono definire nell'insieme delle proposizioni sono le seguenti:
1. La congiunzione logica "AND" ... e
2. La disgiunzione inclusiva "OR" ... o
3. La disgiunzione esclusiva "EOR" ... aut
4. La negazione logica "NOT" ... non
5. L'implicazione logica "se ... allora" che si indica con →
6. La coimplicazione logica "... se e solo se ..." che si indica con ↔
| Operatori logici fondamentali | Simbolismo | ||
| Latino | Hilbert | Informatico | |
| La congiunzione logica | A = A1 et A2 | A = A1 ∧ A2 | A = A1 AND A2 |
| La disgiunzione inclusiva | A = A1 vel A2 | A = A1 ∨ A2 | A = A1 OR A2 |
| La negazione logica | A = non A1 | A = Ã1 | A = NOT A1 |
Tutte queste operazioni sono binarie ad eccezione della negazione logica che è unitaria, nel senso che si applica ad una sola proposizione anzichè a due. Di questi operatori, tre sono particolarmente importanti e cioè e, o, non, poichè ogni altro connettivo può essere derivato da loro e per questo si chiamano connettivi logici fondamentali. Si rappresentano con una delle modalità indicate nella tabella. Il primo deriva dal latino, il secondo è dovuto al matematico Hilbert, il terzo è tratto dalla lingua inglese ed è utilizzato nei linguaggi informatici di programmazione. Quello che utilizzeremo più frequentemente sarà il simbolismo di Hilbert. Per rendersi conto dell'opportunità di questo simbolismo, teniamo presente che lo scopo è quello di ridurre la complessità del linguaggio comune. Si introducono quindi pochi connettivi logici che permettono di esprimere qualsiasi proposizione composta. Questo modo di procedere, ci fa perdere alcune sfumature di significato, ma ci permetterà di raggiungere una formalizzazione non ambigua dei modi di collegare le proposizioni.
Esempio:
1. Giorgio mangia il gelato mentre legge il giornale
2. Giorgio mangia il gelato ma legge anche il giornale
3. Giorgio mangia il gelato e legge il giornale
Queste tre frasi hanno lo stesso significato, le tre congiunzioni mentre, ma, e hanno il ruolo di connettivi, servono cioè a collegare due frasi. Da un punto di vista logico considereremo l'unico connettivo di congiunzione "e" che indicheremo con il simbolo ∧ (AND).
La congiunzione logica AND
E' una operazione di composizione binaria interna che, applicata alla coppia ordinata P1, P2 di proposizioni, dà come risultato una proposizione composta P, ottenuta collegando P1 con P2 mediante la congiunzione e. Il risultato è quindi P=P1∧P2. Ci si chiede ora come varia il valore di verità della proposizione composta P=P1∧P2 in funzione dei valori di verità che possono assumere le proposizioni atomiche P1, P2. Per definizione si ha che la proposizione molecolare P=P1∧P2 risulti vera se e solo se le proposizioni P1, P2, sono contemporaneamente vere. La tavola di verità dell'operatore AND si presenta, come nella tabella di fianco.
| P1 | P2 | P1 ∧ P2 |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Il connettivo AND e l'intersezione insiemistica
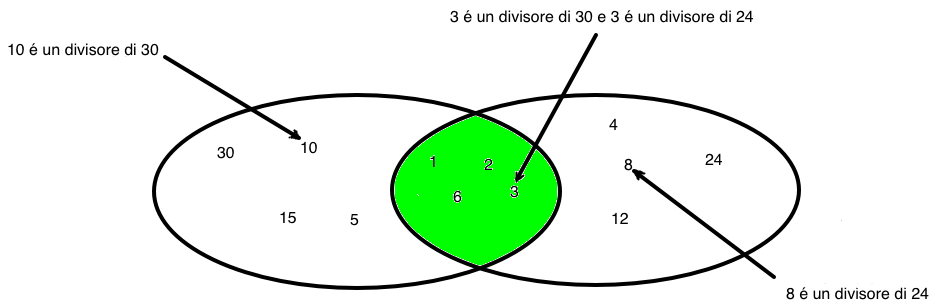
Esiste una stretta relazione tratra l'intersezione insiemistica e il connettivo logico AND. Partiamo da un esempio. Sia A l'insieme dei divisoridi 30 e B l'insieme dei divisori di 24.
Si noti che l'affermazione
10 ∈ A
significa che la proposizione 10 è un divisore di 30 è vera e l'affermazione
4 ∈ A
significa ch la proposizione 4 è un divisore di 24 è vera. Infine
3 ∈ A ∩ B
significa che la proposizione
3 è un divisore di 30 ∧ 3 è un divisore di 24 è vera
Possiamo allora concludere che l'operazione di intersezione di insiemi è corrispondente all'operazione logica di congiunzione
Il connettivo logico OR
Un altro modo di collegare proposizioni atomiche consiste nell'uso del connettivo OR (∨). OR applicato alla coppia ordinata di proposizioni P1, P2 dà come risultato una nuova proposizione composta P = P1 ∨ P2.
Ci si domanda come varia il valore di verità di P in funzione dei valori di verità che si possono attribuire alle proposizioni atomiche P1, P2.
Per definizione, si ha che la proposizione composta P = P1 ∨ P2 risulta vera se e solo se almeno una delle proposizioni atomiche P = P1, P2 è vera.
| P1 | P2 | P1 ∨ P2 |
| V | V | V |
| V | F | V |
| F | V | V |
| F | F | F |
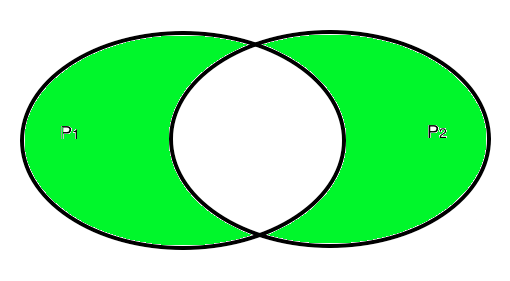
Il connettivo logico OR e l'unione insiemistica
Anche tra il connettivo logico OR e l'oprazione di unione insiemistica esiste una stretta relazione. Partiamo da un esempio. Sia A l'insieme dei rettangoli e B l'insieme dei rombi. Siano inoltre f, g, h tre figure date. Si noti che l'affermazione f ∈ A significa che la proposizione "f è un rettangolo" è vera. D'altra parte g ∈ B, significa che la proposizione "g è un rombo" è vera. Infine h ∈ A ∨ B, significa che la proposizione "h è un rettangolo ∨ h è un rombo" è vera.
La disgiunzione esclusiva EOR (Exclusive OR)
E' un operazione di composizione binaria interna che, applicata alla coppia ordinata P1, P2 di proposizioni, dà come risultato una nuova proposizione composta ottenuta collegando P1 con P2. Il risultato è quindi P = P1 EOR P2. Il valore di verità di P per definizione risulta vera se e solo se una soltanto delle proposizioni P1, P2 risulta vera come descritto dalla tabella di verità riportata di fianco. Seguono alcuni esempi:
P1: l'anno prossimo mi iscrivo alla facoltà di matematica P2: l'anno prossimo mi iscrivo alla facoltà di fisica
P' = P1 EOR P2
P3: Mario ha studiato l'inglese a scuola P4: Mario ha trascorso un lungo periodo in Inghilterra
P'' = P3 OR P4
| P1 | P2 | P1 EOR P2 |
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Nella proposizione P' si è usato EOR in quanto P1 esclude P2. Nel comporre la proposizione P'' invece si è usato OR poichè la proposizione P3 non esclude la P4 ovvero Mario potrebbe parlare bene l'inglese in quanto lo ha studiato a scuola oppure perchè è stato un lungo periodo in Inghilterra, oppure perchè ha fatto tutte due queste cose.
Il connettivo EOR e la differenza simmetrica
L'oppure esclusivo EOR è gia stato considerato nella teoria degli insiemi, per definire l'operazione di differenza simmetrica. Esiste quindi una stretta analogia tra l'operatore logico EOR (aut), che si utilizza per comporre una coppia di proposizioni, e l'operazione di differenza simmetrica, usata per comporre due insiemi.
La negazione logica (NOT)
L'operazione di negazione logica NOT è detta unitaria poichè si applica su una sola proposizione A1 e dà come risultato una nuova proposizione A, A = Ã1 (A = NOT A1), così definita: il valore di verità di A è l'inverso del valore di verità di A1. La relativa tabella di verità è riportata a fianco. Di seguito un esempio:
A1: "Arezzo è il capoluogo della Toscana" proposizione il cui valore di verità è falso.
Ã1: "Arezzo non è il capoluogo della Toscana", il cui valore di verità è vero, ossia l'inverso di quello di A1
| A1 | Ã1 |
| F | V |
| V | F |
La negazione logica e l'insieme complementare
Sia A l'insieme dei numeri pari e N l'insieme universo. Il complementare di A è l'insieme dei numari dispari O. Si noti che 4 ∈ A, significa che la proposizione "4 è pari" è vera mentre 3 ∈ Ã significa che la proposizione "3 non è pari" è vera. Esiste quindi una stretta analogia tra l'operatore logico non che si applica ad una proposizione e il complementare di un insieme rispetto al suo ambiente.
L'implicazione materiale
E' un'operazione che, applicata alla coppia ordinata (P1,P2) di proposizioni dà per risultato una nuova proposizione P=P1→P2 i cui valori di verità dipendono unicamente da quelli assunti dagli operandi P1,P2 secondo una predefinita tavola di verità. Si osservi che le proposizioni P1,P2, in generale sono autonome una rispetto all'altra, nel senso che non si richiede alcuna correlazione tra l'argomento di cui tratta la P1, e quello che interessa la P2, inoltre P1 e P2, possono essere anche false.
Consideriamo come esempio una proposizione tratta dal linguaggio comune: "Se piove andiamo al cinema".
Assumendo come vera questa proposizione siamo portati a considerare come ammissibili tre situazioni:
1. Piove e quindi andiamo al cinema. 2. Non piove e non andiamo al cinema. 3. Non piove e andiamo al cinema.
| P1 | P2 | P1 → P2 |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
La nostra affermazione ci lascia in effetti liberi di andare o non andare al cinema se non piove. Equivalentemente possiamo dire che l'affermazione "se piove andiamo al cinema" sarà falsa solo nel caso in cui piova e non si vada al cinema. Nella frase possiamo distinguere una prima proposizione, "se piove", che chiameremo antecedente e una seconda, "andiamo al cinema", che chiameremo conseguente. Date le osservazioni precedenti consideremo vera l'implicazione materiale se:
1. L'antecedente ed il conseguente sono falsi. 2. L'antecedente ed il conseguente sono veri. 3. L'antecedente è falso ed il conseguente è vero.
Il connettivo di implicazione materiale se ... allora ... lo indicheremo con il simbolo →. La proposizione p → q, sarà vera secondo la tavola di verità.
La deduzione logica
E' un ragionamento che costituisce la base della dimostrazione di un qualsiasi teorema. L'enunciato di un teorema si presena sempre nella forma seguente: se h allora t ovvero da h si deduce t ove le proposizioni h e t sono rispettivamente , ipotesi e tesi. Precisiamo che la deduzione logica è costituita dalla successione di ragionamenti, intuizioni, osservazioni e calcoli logicamente corretti che, a partire dalla verità dell'ipotesi h, conduce ad affermare che anche la tesi è vera, a differenza dell'implicazione materiale, in quanto non avrebbe alcun significato un teorema che avesse l'ipotesi falsa. Inoltre, in generale, gli argomenti trattati in h e t sono omogenei, cioè della stessa naturae correlati l'uno all'altro, in ogni caso l'implicazione materiale e la deduzione logica presentano analogie ad esempio sono entrambe non commutative e godono della proprietà transitiva ovvero: se P1 → P2, e P2 → P3 allora P1 → P3
La deduzione logica e relazione di inclusione tra insiemi
Possiamo osservare che esiste un ben preciso collegamento tra la deduzione logica e la relazione di inclusione insiemistica. Si noti infatti che, se se A e B sono due insiemi, l'affermazione A ⊆ B equivale a dire che l'implicazione x ∈ A → x ∈ B è vera comunque si scelga un elemento x di A (∀ x ∈ A). E' bene sottolineare che in una implicazione è importante l'ordine in cui sono date le due proposizioni (non commutatività), infatti dalla veridicità dell'implicazione p → q non discende affatto che sia vera la q → p.
Esempio
p: Mario è nato a Milano, q: Mario è lombardo, p → q è vera, q → p non è detto che sia vera. Ciò è evidente anche dal punto di vista insiemistico.
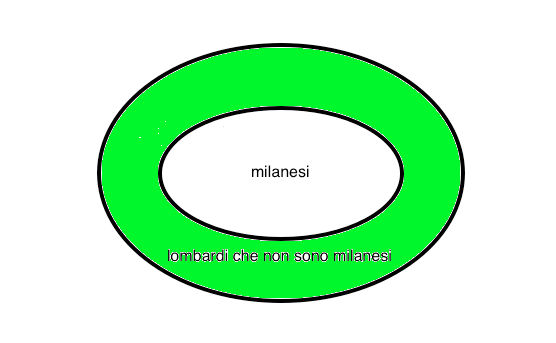
Nel caso in cui due proposizioni si implichino a vicenda, cioè nel caso in cui siano vere sia p → q che q → p parleremo di doppia implicazione o equivalenza logica che indicheremo con il simbolo ∀. L'equivalenza logica corrispode alla coincidenza di insiemi, infatti A = B significa che la doppia implicazione x ∈ A ∀ x ∈ B è vera comunque si scelga un elemento x di A o di B.
La doppia deduzione logica
La doppia deduzione logica è una procedura in base alla quale, assegnate due proposizioni h e t, si può dimostrare che: Teorema 1 "da h, vera per ipotesi, si deduce, tramite ragionamenti logici, che anche la t è vera." Teorema 2 "da t, vera per ipotesi, si deduce, tramite ragionamenti logici, che anche la h è vera." Quest'ultimo è il teorema inverso del teorema 1, in quanto è stato ottenuto scambiando l'ordine delle proposizzioni h e t. Un teorema ed il suo inverso si possono unificare in un teorema complessivo il cui enunciato è del tipo seguente: " h è vera se e solo se t è vera" ove le proposizioni h e t sono dette logicamente equivalenti. Il teorema complessivo si enuncia, a volte secondo quest'altra formulazione: "Condizione necessaria e sufficiente affinchè h sia vera e che t sia vera." La condizione necessaria è espressa dal teorema diretto, "Da h vera si deduca t vera", la condizione sufficiente è rappresentata dal teorema inverso "Da t vera si deduca h vera".
Connettivi definibili a partire da quelli fondamentali
I connettivi logici fondamentali sono AND, OR, NOT. Ogni altro connettivo può essere derivato da questi. Ci proponiamo allora di dimostrare a titolo d'esempio, la derivabilità dell'implicazione logica e della disgiunzione esclusiva dai connettivi fondamentali. Nel procedere ci renderemo anche conto che i connettivi logici possono collegare tra di loro non solo proposizioni atomiche, ma anche proposizioni molecolari. E' quindi possibile produrre proposizioni via via più complesse. Consideriamo la proposizione ã ∨ n. Si osservi che il primo termine ã non è una proposizione atomica, ma la negazione della proposizione a. D'ora in poi ci si atterrà alla convenzione secondo cui l'operatore di negazione ha priorità sugli altri connettivi, va cioè considerato prima di ogni altro connettivo. Costruiamo la tavola di verità di ã ∨ n.
| a | n | ã | ã ∨ n |
| V | V | F | V |
| V | F | F | F |
| F | V | V | V |
| F | F | V | V |
| a | n | a → n |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Se ora togliamo dalla tavola la terza colonna, che ci è servita solo come di passaggio intermedio otteniamo una nuova tabella che ha gli stessi valori di quella dell'implicazione a → n. Ciò dimostra l'equivalenza logica delle proposizioni ã ∨ n e a → n. D'altra parte, anche dal punto di vista del linguaggio comune le due proposizioni sono equivalenti.
Ad esempio l'affermazione "se piove andiamo al cinema" è vera quando (e solo quando) è vera la proposizione "non piove o andiamo al cinema".
Mostriamo ora che la disgiunzione esclusiva EOR è equivalente alla proposizione (ã ∧ n) ∨ (a ∧ ñ) che, come si nota utilizza solo i tre connettivi fondamentali. Costruiamo le due tavole di verità e, considerando solo la prima la seconda e l'ultima colonna di entrambe, notiamo che sono equivalenti.
| a | n | ã | ñ | ã ∨ n | a ∧ ñ | (ã ∧ n) ∨ (a ∧ ñ) |
| V | V | F | F | F | F | F |
| V | F | F | V | F | V | V |
| F | V | V | F | V | F | V |
| F | F | V | V | F | F | F |
| a | n | a EOR n |
| V | V | F |
| V | F | V |
| F | V | V |
| F | F | F |
Algebra del ragionamento
La logica cerca di stabilire il valore di verità e la correttezza di un ragionamento, in base alla applicazione corretta delle leggi della deduzione logica. Formalizzare un ragionamento significa scomporlo in enunciati semplici collegati dai connettivi logici. Analizziamo un ragionamento che si vuole formalizzare dal punto di vista logico:
"Se il bilancio non subisce tagli, allora condizione necessaria e sufficiente perchè i prezzi rimangano stabili è che le tasse vengano aumentate. Le tasse verranno aumentate solo se il bilancio non subisce tagli. Se i prezzi rimangono stabili allora le tasse non saranno aumentate. Quindi le tasse non verranno aumentate."
Se si volesse stabilire la correttezza del ragionamento fatto, solo in base ad una comprensione linguistica del testo, sarebbe alquanto difficile. Individuiamo allora le variabili proposizionali all'interno del testo:
a1 = "Il bilancio subisce tagli" a2 = "I prezzi rimangono stabili" a3 = "Le tasse vengono aumentate"
Traduciamo nel linguaggio simbolico della logica, le diverse asserzioni che compongono il testo:
(1) prima asserzione: ã1 → (a2 ↔ a3) (2) seconda asserzione: a3 → ã1 (3) terza asserzione: a2 → ã3 (4) conclusione: ã3
La struttura del testo è quindi data dalla seguente espressione logica:
(5) ((ã1 → (a2 ↔ a3)) ∧ (a3 → ã1) ∧ (a2 → ã3)) → (ã3)
Per esaminare la correttezza della deduzione logica che caratterizza questo ragionamento, costruiamo la tavola di verità dell'espressione che, contenendo tre variabili proposizionali a1, a2, a3, sarà formata da otto righe.
| a1 | a2 | a3 | ã1 | a2 ↔ a3 | (1): ã1 → (a2 ↔ a3) | (2): a3 → ã1 | (3): a2 → ã3 | ã3 | (1)∧(2)∧(3) | (5) |
| F | F | F | V | V | V | V | V | V | V | V |
| F | F | V | V | F | F | V | V | F | F | V |
| F | V | F | V | F | F | V | V | V | F | V |
| F | V | V | V | V | V | V | F | F | F | V |
| V | F | F | F | V | V | V | V | V | V | V |
| V | F | V | F | F | V | F | V | F | F | V |
| V | V | F | F | F | V | V | V | V | V | V |
| V | V | V | F | V | V | F | F | F | F | V |
Come si vede nell'ultima colonna della tabella di verità, si tratta di una tautologia, che è sempre vera per qualsiasi valore di verità che venga assegnato alle variabili proposizionali. Tramite questo esempio si può capire che il ragionamento, grazie alle leggi della logica, può essere tradotto in espressioni algebriche e queste possono essere calcolate da un automa. In quale modo il calcolo proposizionale può essere automatizzato viene descritto nel paragrafo dedicato all'algebra di Bool.