Retta

esercizio guida: distanza punto retta

Supponiamo che i dati del problema siano le coordinate di un punto P e l'equazione di una retta r. La consegna dell'esercizio è quella di determinare la distanza del punto P dalla retta r. Quindi in sucessione:

  • estrapolare il coefficiente angolare della retta r
  • determinare il coefficiente della perpendicolare
  • determinare l'equazione della retta s perpendicolare, passante per P
  • determinare il punto di intersezione Q, mettendo a sistema le rette r, s
  • determinare la distanza del punto P dal punto Q con la relativa formula

    • esercizio guida: baricentro di un triangolo

    Supponiamo che i dati del problema siano le coordinate dei vertici A, B, C del triangolo. Tenendo presente che il baricentro è il punto di intersezione delle tre mediane bisogna determinare l'equazione di due delle tre mediane del triangolo. Quindi in sucessione:

  • determinare il punto medio M di un lato, per esempio del lato AB
  • determinare il punto medio N di un altro lato, per esempio del lato AC
  • determinare l'equazione della mediana CM
  • determinare l'equazione della mediana BN
  • trovare il baricentro G, mettendo a sistema l'equazioni delle due mediane
  • verificare che la distanza CG sia il doppio della distanza GM
  • verificare che la distanza BG sia il doppio della distanza GN

    • esercizio guida: area del triangolo

    Supponiamo che i dati del problema siano le coordinate dei vertici A, B, C del triangolo. Tenendo presente che l'area del triangolo è data dalla metà del prodotto della misura della base moltiplicata per l'altezza bisogna determinare base ed altezza del triangolo quindi in sucessione:

  • determinare la misura della base, per esempio del lato AB
  • determinare l'equazione della retta AB
  • individuare il coefficiente angolare della retta AB
  • determinare l'equazione della retta passante per C perpendicolare alla retta AB, tenendo presente che il coefficiente angolare di tale retta è opposto e reciproco a quello della retta AB
  • trovare il piede dell'altezza H, mettendo a sistema l'equazioni delle due rette determinate in precedenza
  • determinare la distanza CH che corrisponde all'altezza del triangolo
  • moltiplicare base per altezza e dividere per 2 per individuare l'area del triangolo

    • esercizio guida: circocentro del triangolo

    Supponiamo che i dati del problema siano le coordinate dei vertici A, B, C del triangolo. Tenendo presente che il circocentro è il punto di intersezione dei tre assi bisogna determinare l'equazione di due dei tre assi del triangolo. Quindi in sucessione:

  • determinare il punto medio M di un lato, per esempio del lato AB
  • determinare il punto medio N di un altro lato, per esempio del lato AC
  • determinare il coefficiente angolare della retta AB
  • determinare il coefficiente angolare della retta AC
  • determinare l'equazione dell'asse CM tenendo presente che il relativo coefficiente angolare dev'essere opposto e reciproco a quello della retta AB
  • determinare l'equazione dell'asse BN tenendo presente che il relativo coefficiente angolare dev'essere opposto e reciproco a quello della retta AC
  • trovare il circocentro O, mettendo a sistema l'equazioni dei due assi trovati in precedenza
  • verificare che la distanza OA sia uguale alla distanza OB e OC

    • esercizio guida: determinazione del quarto vertice di un parallelogramma

    Supponiamo che i dati del problema siano le coordinate di tre vertici A, B, C di un parallelogramma di cui si vuol determinare il quarto vertice D. Tenendo presente che i lati opposti di un parallelogramma sono paralleli bisogna determinare le equazioni delle due rette CD e AD e metterle a sistema. Quindi in sucessione:

  • determinare l'equazione della retta AB
  • determinare l'equazione della retta BC
  • determinare l'equazione della retta AD tenendo presente che il relativo coefficiente angolare dev'essere uguale a quello della retta BC
  • determinare l'equazione della retta CD tenendo presente che il relativo coefficiente angolare dev'essere uguale a quello della retta AB
  • trovare il vertice D, mettendo a sistema l'equazione delle due rette AD e CD trovate in precedenza
  • verificare che la distanza AB sia uguale alla distanza DC
  • verificare che la distanza AD sia uguale alla distanza BC

    • esercizio guida: asse di un segmento

    Determinare l'equazione dell'asse del segmento di estremi A(3,1) e B(5,6).

    Siccome tutti e solo i punti dell'asse godono della proprietà di essere equidistanti dagli estremi del segmento, consideriamo un punto dell'asse P(x,y) di coordinate generiche e imponiamo che la distanza d(A,P) sia uguale alla distanza d(B,P):


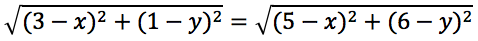
    Quadriamo ovvero eleviamo al quadrato entrambi i membri dell'equazione:


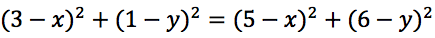
    Sviluppiamo i quadrati:


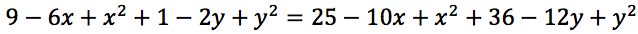
    Semplifichiamo e trasportiamo i termini noti e i termini con le variabili "x" al secondo membro notando che si tratta di un'equazione di primo grado a due incognite:


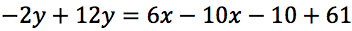
    Sommiamo i termini simili:


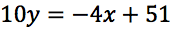
    Si tratta dell'equazione dell'asse del segmento AB, scriviamola in forma esplicita:

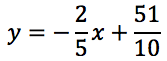
    esercizio guida: deduzione dell'equazione della retta dall'analisi del grafico

    Vediamo come si possa dedurre l'equazione della retta in figura senza fare alcun calcolo, ma semplicemente dall'analisi del grafico.


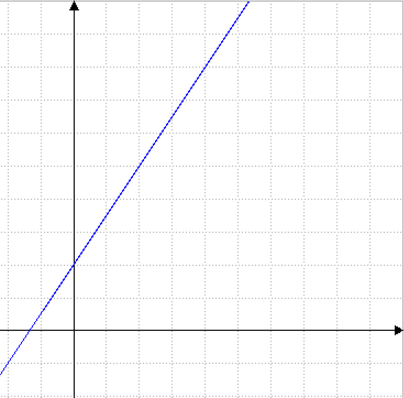
    Nel grafico di sopra, si noti che per ogni incremento di due quadrattini sull'asse "x" la retta incrementa di 3 quadrattini sull'asse "y", da ciò si può dedurre che il coefficiente angolare risulta 3/2. Si noti che la retta interseca l'asse delle "y" nel punto di coordinate (0,2), da ciò si può dedurre che il termine noto risulta 2. l'equazione della retta sarà quindi y=(3/2)x+2.


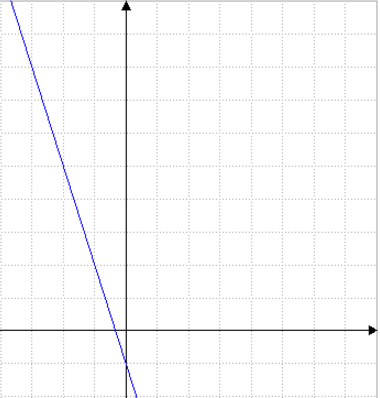
    Nel grafico di sopra, si noti che per ogni incremento di un quadrattino sull'asse "x" la retta decrementa di 3 quadrattini sull'asse "y", da ciò si può dedurre che il coefficiente angolare risulta -3. Si noti che la retta interseca l'asse delle "y" nel punto di coordinate (0,-1), da ciò si può dedurre che il termine noto risulta -1. l'equazione della retta sarà quindi y=(-3)x-1

    esercizi

    1. Determinare il baricentro del triangolo di vertici A(3,8), B(-1,-2) e C(4,-1)
      [G(2,5/3)]

    2. Determinare il baricentro del triangolo di vertici A(5,1), B(1,8) e C(0,0)
      [G(2,3)]

    3. Determinare il perimetro del triangolo di vertici A(3,8), B(-1,-2) e C(4,-1)
      [2√29+√82+√26]

    4. Determinare il circocentro del triangolo di vertici 0(0,0), A(5,1) e B(2,8)
      [C(35/19,72/19)]

    5. Determinare il circocentro del triangolo di vertici A(-1,2) B(-9,2) e C(-5,-1)
      [(-5,19/6)]

    6. Determinare l'equazione della retta passante per A(2,0) e B(1\2,-3\4)
      [y=(1/2)x-1]

    7. Determinare le coordinate del punto di intersezione dell'asse del segmento di estremi A(0,-1) e B (2,1) con la retta di equazione 2x+y+2=0
      [(-3,4)]

    8. Determinare le coordinate del punto di intersezione dell'asse del segmento di estremi A(3,-1) e B (4,2) con la retta di equazione 2x-y-1=0
      [(8/7,9/7)]

    9. Determinare l'equazione della retta perpendicolare alla retta AB, con A(2,5), B(-3,-1) e passante per il punto C(-2,3)
      [y=(-5\6)x+(4/3)]

    10. Determinare l'equazione della retta passante per A(2,0) e B(-3,-5\2)
      [y=(1\2)x-1]

    11. Determinare l'equazioni delle rette passanti per A(1,-1), parallela e perpendicolare alla retta 2x+y-8=0
      [y=(1\2)x-3/2 y=-2x+1]

    12. Determinare l'equazioni delle rette passanti per A(1,-1), parallela e perpendicolare alla retta y=(1/4)x
      [y=(1\4)x-5/4 y=-4x+3]

    13. Determinare l'asse del segmento di estremi A(1,8) e B(2,7)
      [y=x+6]

    14. La retta di equazione 4x+3y-12=0 interseca gli assi cartesiani in due punti A e B, determinare area e perimetro del triangolo AOB dove O è l'origine del sistema di riferimento
      [S=6, 2P=12]

    15. Determinare il punto A della retta y=3x+5 equidistante dai punti B(3,1) e C(2,-1)
      [A(-15/14,25/14)]

    16. Determinare il punto A della retta y=2x-1 equidistante dai punti B(3-,1) e C(4,2)
      [A(8/7,9/7)]

    17. Determinare la distanza del punto P(1,2) dalla retta y=2/3x-2
      [(10√13)/13]

    18. I punti A=(1,4) B=(-3,1) C=(5,-1) siano tre vertici consecutivi di un parallelogramma. Trovare le coordinate del quarto vertice.
      [D(9,2)]

    19. I punti A=(1,1) B=(3,5) C=(8,2) siano tre vertici di un triangolo. Determinare l'area del triangolo.
      [13]


    Coniche

    esercizio guida: equazione della parabola dati fuoco e direttrice

    Determinare l'equazione della parabola avente per fuoco F(2,5) e per direttrice la retta di equazioney=1

    Sia il punto P un punto della parabola avente coordinate generiche x e y. Chiamiamo H il piede dell'altezza che insiste sulla direttrice e che ha quindi coordinate (x,1). Tenendo presente che la parabola è il luogo geometrico in cui tutti e solo i suoi punti sono equidistanti dal fuoco e dalla direttrice, imponiamo che d(F,P)=d(P,H) ovvero:

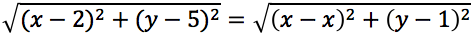
    quadrando e sviluppando i quadrati si ottiene:

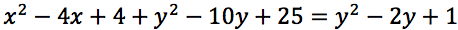
    esplicitando si ottiene:

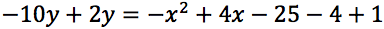
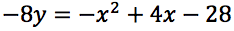
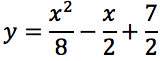
    esercizio guida: equazione della parabola per tre punti

    Determinare l'equazione della parabola ad asse verticale passante per A(0,-3), B(1,0), C(-1,-4)

    Scriviamo l'equazione di una parabola ad asse verticale: y=ax2+bx+c, sostituiamo alle incognite x e y le coordinate dei tre punti dati e otteniamo un sistema di primo grado di incognite a, b, c.

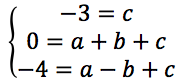
    risolviamo il sistema sostituendo la c:

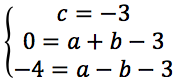
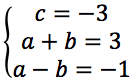
    sommiamo le ultime due equazioni e ricopiamo la prima delle due:

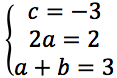
    nella terza equazione per determinare b si è sostituito all'incognita a il valore 1.

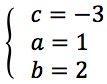
    esercizio guida: equazione dell'ellisse

    esercizio guida: equazione della tangente alla parabola

    esercizio guida: equazione dell'iperbole

    esercizi

    1. Determinare l'equazione della parabola ad asse verticale passante per A(0,3), B(1,0), C(-1,-2)
      [y=-4x2+x+3]

    2. Determinare l'equazione della parabola ad asse verticale avente per fuoco il punto (-1,2), e direttrice la retta di equazione y=3/2.
      [y=x2+2x+11/4]

    3. Determinare l'equazione della circonferenza passante per i punti A(3,4), B(0,-5), C(-2,-1).
      [x2+y2-6x+2y-15=0]

    4. Determinare l'equazione della circonferenza passante per i punti A(1,0), B(2,1), C(-2,-1).
      [x2+y2+4x-8y-5=0]

    5. Determinare l'equazione della circonferenza passante per i punti A(3,1), B(0,2), C(3,5).
      [x2+y2-(17/3)x+(13/3)y+14/3=0]

    6. Determinare l'equazione della circonferenza avente per diametro il segmento AB con A(2,1), B(6,5).
      [(x-4)2+(y-3)2=8]

    7. Determinare l'equazione della circonferenza passante per i punti A(3,1), B(1,3), C(1,-1).
      [x2+y2-2x-2y-2=0]

    8. Determinare l'equazione della tangente alla parabola di equazione y=x2+1 nel punto di ascissa x=-1.
      [y=-2x]

    9. Determinare l'equazione della tangente alla parabola di equazione y=x2+1 nel punto di ascissa x=1.
      [y=2x]

    10. Determinare l'equazione della tangente alla parabola di equazione y=x2+3 nel punto di ascissa x=2.
      [y=4x-1]

    11. Determinare centro e raggio della circonferenza passante per i punti A(0,3), B(1,0), C(-1,-2).
      [C(-7/4,3/4) r=√130/16]